ያለ ካልኩሌተር የካሬ ሥሮችን ለማግኘት 3 መንገዶች

2024 ደራሲ ደራሲ: Jason Gerald | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2023-12-16 10:52

የአንድ ቁጥር ካሬ ሥሩ መልሱ ኢንቲጀር ከሆነ በቀላሉ ማግኘት ይቻላል። መልሱ ኢንቲጀር ካልሆነ ፣ ካልኩሌተር ባይጠቀሙም የካሬውን ሥር ለማግኘት የሚከተሏቸው ተከታታይ ሂደቶች አሉ። ለዚያም የማባዛት ፣ የመደመር እና የመከፋፈል መሰረታዊ ነገሮችን መረዳት ያስፈልግዎታል።

ደረጃ

ዘዴ 1 ከ 3 - የአንድ ኢንቲጀር ካሬ ሥር መፈለግ

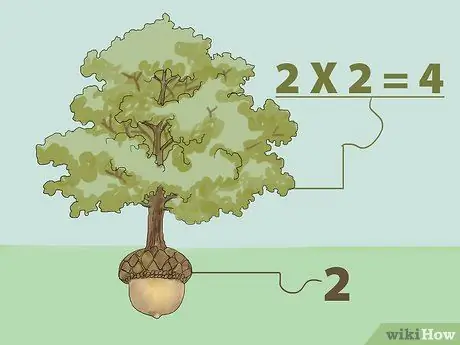
ደረጃ 1. በማባዛት ትክክለኛውን ካሬ ሥር ይፈልጉ።

የቁጥር ካሬ ሥሩ በራሱ ሲባዛ የመጀመሪያውን ቁጥር የሚመልስ ቁጥር ነው። በሌላ አነጋገር - "የምንፈልገውን ቁጥር ለማግኘት በራሱ ስንት ቁጥር ማባዛት እንችላለን?"

• ለምሳሌ ፣ 1 በ 1 ሲባዛ 1 (1X1 = 1) ስለሆነ የ 1 ካሬ ሥሩ 1 ነው። ስለዚህ ፣ የ 4 ካሬ ሥሩ 2 ነው ምክንያቱም 2 በ 2 ተባዝቶ 4 (2X2 = 4) ነው። የካሬው ሥር ጽንሰ -ሀሳብ እንደ ዛፍ ያስቡ። አንድ ዛፍ ከዘር ያድጋል። ስለዚህ ፣ አንድ ዛፍ ከዘር ይበልጣል ፣ እሱም ሥሩ ከሆነው ዘር ይበቅላል። ከላይ ከተጠቀሰው ምሳሌ 4 ዛፉ ሲሆን 2 ዘር ነው።
• ስለዚህ ፣ የ 9 ካሬ ሥሩ 3 (3X3 = 9) ፣ 16 ከ 4 (4X4 = 16) ፣ ከ 25 5 (5X5 = 25) ፣ ከ 36 6 (6X6 = 36) ፣ 49 ነው 7 (7X7 = 49) ፣ ከ 64 8 (8X8 = 64) ፣ ከ 81 9 (9X9 = 81) ፣ እና ከ 100 10 (10X10 = 100)።

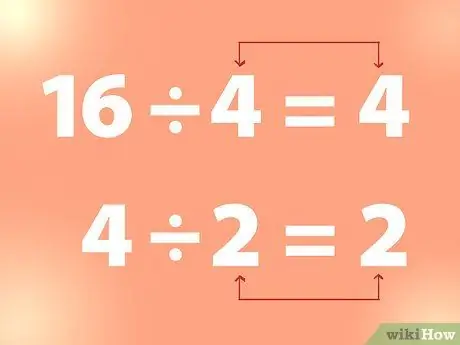
ደረጃ 2. የካሬውን ሥር ለማግኘት ቀጣይ ክፍፍልን ይጠቀሙ።

የአንድ ኢንቲጀር ካሬ ሥር ለማግኘት ፣ ከፋይውን የሚያክል ቁጥር እስኪያገኙ ድረስ ኢንቲጀሩን በቁጥር መከፋፈል ይችላሉ።

• ምሳሌ 16 በ 4 የተከፈለ ነው 4. እና 4 በ 2 የተከፈለ 2 ነው ፣ ወዘተ. ስለዚህ ፣ ከላይ ከተጠቀሰው ምሳሌ ፣ 4 የካሬው ሥር 16 እና 2 የ 4 ካሬ ሥሩ ነው።
• ፍጹም ካሬ ሥሮች ሙሉ ቁጥሮች ስለሆኑ ምንም ክፍልፋዮች ወይም አስርዮሽ የላቸውም።

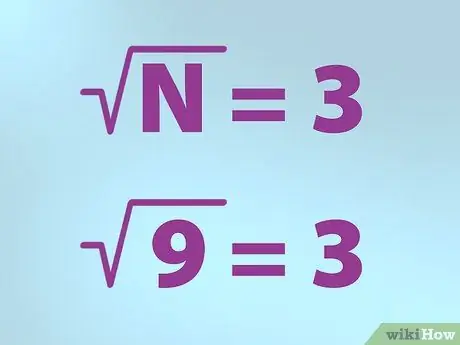
ደረጃ 3. ለካሬው ሥር ትክክለኛውን ምልክት ይጠቀሙ።

የሂሳብ ሊቃውንት የካሬ ሥሩን ለመወከል ልዩ ምልክት ይጠቀማሉ። ቅርጹ ከላይ በስተቀኝ መስመር ሲደመር እንደ ቼክ ምልክት ነው።

• N የካሬ ሥሩን ለማግኘት ከሚፈልጉት ቁጥር ጋር እኩል ነው። N በቼክ ምልክት ስር ይቀመጣል።
• ስለዚህ ፣ የ 9 ካሬ ሥሩን ማግኘት ከፈለጉ ፣ “N” (9) በቼክ ምልክት (ምልክት “ሥር”) ውስጥ በማስቀመጥ ቀመር ይፃፉ እና ከዚያ እኩል ምልክት ይፃፉ እና ይከተሉታል። 3. ይህ ማለት “ካሬ ሥር 9 ከ 3 "ጋር እኩል ነው።

ዘዴ 2 ከ 3 - የሌላውን ቁጥር ካሬ ሥር መፈለግ

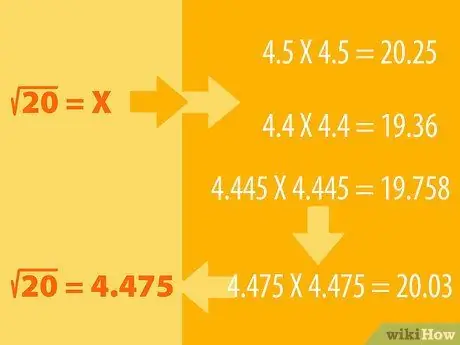
ደረጃ 1. መገመት እና የማስወገድ ሂደቱን ያድርጉ።

ኢንቲጀር ያልሆነ ቁጥር ካሬ ሥር ማግኘት አስቸጋሪ ነው። ሆኖም ፣ ያ ማለት አይቻልም ማለት አይደለም።

• ለምሳሌ ፣ የ 20 ካሬ ሥሩን ማግኘት እንደሚፈልጉ ይናገሩ 16 እኛ ካሬ ስሩ 4 (4X4 = 16) የሆነ ፍጹም ካሬ መሆኑን እናውቃለን። ከዚያ 25 ካሬ ሥሮች 5 (5X5 = 25) ናቸው ፣ ስለዚህ የ 20 ካሬ ሥሩ በሁለቱ መካከል መተኛት አለበት።
• የ 20 ካሬ ሥሩ 4.5 ነው ብለው መገመት ይችላሉ። ውጤቱን ለማየት አሁን ካሬ 4.5። ያም ማለት 4 ፣ 5 ን በእራሱ እናባዛለን ፣ 4 ፣ 5X4 ፣ 5. መልሱ ከ 20 በላይ ወይም ያነሰ ከሆነ ይመልከቱ። የእርስዎ ግምት በጣም ሩቅ ከሆነ ፣ ሌላ ቁጥር ይሞክሩ (ለምሳሌ 4 ፣ 6 ወይም 4 ፣ 4) እና ያስተካክሉ በዚህ መሠረት ግምቱን። እርስዎ ቁጥር 20 እስኪያገኙ ድረስ።
• ለምሳሌ ፣ 4 ፣ 5X4 ፣ 5 = 20 ፣ 25 ፣ ስለዚህ በሎጂክ አነስ ያለ ቁጥር ማግኘት አለብን ፣ ምናልባት 4 ፣ 4. 4 ፣ 4X4 ፣ 4 = 19 ፣ 36. ስለዚህ ፣ የ 20 ካሬ ሥሩ በ 4 መካከል መዋሸት አለበት ፣ 5 እና 4 ፣ 4. በ 4 ፣ 445X4 ፣ 445 ይሞክሩት ውጤቱ 19 ፣ 758. ውጤቱ እየቀረበ ነው። 4 ፣ 475X4 ፣ 475 = 20 ፣ 03 እስኪያገኙ ድረስ በሌሎች ቁጥሮች መሞከርዎን ይቀጥሉ። ተሰብስቦ ፣ ያ ቁጥር 20 ነው።

ደረጃ 2. አማካይ ሂደቱን ይጠቀሙ።

ይህ ሂደትም የሚጀምረው በቁጥር ጎን ለጎን ያሉትን ሁለቱን በጣም ቅርብ የሆኑ ፍጹም ካሬዎችን በማግኘት ነው።

• ከዚያ ያንን ቁጥር በአንድ ፍጹም ካሬ ሥሮች በአንዱ ይከፋፍሉ። መልሱን ይውሰዱ ፣ ከዚያ በዛ ቁጥር እና ሥሩን ለማግኘት በሚፈልጉት ቁጥር መካከል ያለውን አማካይ ያግኙ (ሁለቱን አንድ ላይ በመጨመር እና ለሁለት በመከፋፈል አማካይውን ማግኘት ይችላሉ)። ከዚያ የመጀመሪያውን ቁጥር በተገኘው አማካይ ይከፋፍሉ። የመጨረሻው ደረጃ ፣ የውጤቶቹ አማካኝ ለመጀመሪያ ጊዜ ከተሰላው አማካይ ጋር ያግኙ።
• የተወሳሰበ ድምጽ? ምሳሌ ቢሰጥ ይቀላል። ለምሳሌ ፣ በሁለቱ ፍጹም አደባባዮች 9 (3X3 = 9) እና 16 (4X4 = 16) መካከል 10 ውሸቶች። የሁለቱም ቁጥሮች ካሬ ሥሮች 3 እና 4. ስለዚህ ፣ በመጀመሪያው ቁጥር 10 ን ይከፋፈሉ ፣ 3. ውጤቱን 3 ፣ 33. አሁን 3 እና 3 ፣ 33 አማካይ በመደመር እና በ 2. በመከፋፈል ውጤቱን ያግኙ። ነው 3 ፣ 1667 አሁን 10 ን በ 3.1667 ይከፋፍሉ። ውጤቱ 3.1579 ነው። በመቀጠል በመደመር እና በ 2. በመከፋፈል 3.1579 እና 3.1667 ያግኙ 2. ውጤቱ 3.1623 ነው።
• መልሱን በማባዛት (በዚህ ምሳሌ 3 ፣ 1623) በራሱ ውጤትዎን ይፈትሹ። የ 3.1623 ውጤት በ 3.1623 ተባዝቶ 10.001 ሆኗል።

ዘዴ 3 ከ 3 - አሉታዊ ቁጥሮች

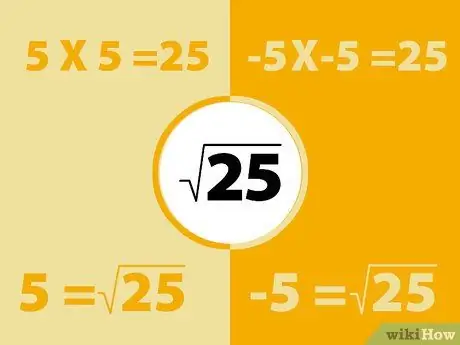
ደረጃ 1. ተመሳሳዩን ዘዴ በመጠቀም ካሬ አሉታዊ ቁጥሮች።

ያስታውሱ አሉታዊ ጊዜያት አሉታዊ አዎንታዊ ናቸው። ስለዚህ ፣ የአሉታዊ ቁጥር ካሬው አዎንታዊ ቁጥርን ያመጣል።

• ለምሳሌ ፣ -5X -5 = 25. ሆኖም ፣ ያንን ደግሞ 5x5 = 25 ያስታውሱ። ስለዚህ የ 25 ካሬ ሥሩ -5 ወይም 5. በመሠረቱ እያንዳንዱ ቁጥር ሁለት ካሬ ሥሮች አሉት።
• በተመሳሳይ ፣ 3X3 = 9 እና -3X -3 = 9 ፣ ስለዚህ የ 9 ካሬ ሥሮች 3 እና -3 ናቸው። አወንታዊው ካሬ ሥሩ “ዋና ሥር” ተብሎ ይጠራል። በዚህ ጊዜ ፣ ለዚህ መልስ ብቻ ትኩረት መስጠት አለብን።

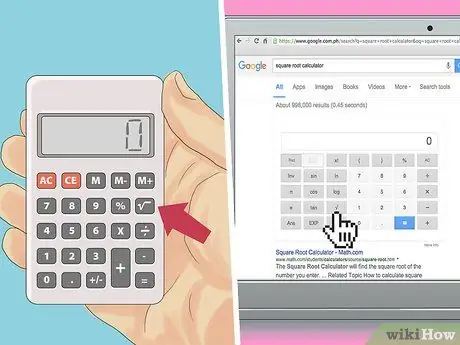
ደረጃ 2. ካልኩሌተር ይጠቀሙ።

ሂሳብን በእጅ ማድረግ መቻል በጣም ጥሩ ቢሆንም ፣ አራት ማዕዘን ሥሮችን ለማስላት ብዙ የመስመር ላይ ካልኩሌተሮች አሉ።

• በመደበኛ ካልኩሌተር ላይ የካሬው ሥር ቁልፍን ይፈልጉ።
• በመስመር ላይ ካልኩሌተር ውስጥ የካሬውን ሥር ዋጋ ለማግኘት የሚፈልጉትን ቁጥር በቀጥታ ያስገቡ እና አዝራሩን ጠቅ ያድርጉ። ኮምፒዩተሩ የካሬው ሥር እሴት ያሳያል።

ጠቃሚ ምክሮች

• ሁል ጊዜ ጥቂት አስፈላጊ የሆኑ ፍጹም ካሬዎችን ያስታውሱ-

  • 0² = 0, 1² = 1, 3² = 9, 4² = 16, 5² = 25, 6² = 36, 7² = 49, 8² = 64, 9² = 81, 10² = 100,
  • እንዲሁም ይህንን ፍጹም ካሬ ያስታውሱ -11² = 121, 12² = 144, 13² 169, 14² = 196, 15² = 225, 16² = 256, 17² = 289…
  • እንዲሁም ይህንን ልብ ይበሉ - 10² = 100, 20² = 400, 30² = 900, 40² = 1600, 50² = 2500, …