ክፍልፋዮችን ማከል እና መቀነስ አስፈላጊ ክህሎት ነው። ክፍልፋዮች በዕለት ተዕለት ሕይወት ውስጥ ሁል ጊዜ ይታያሉ ፣ በተለይም በሂሳብ ትምህርቶች ፣ ከአንደኛ ደረጃ እስከ ኮሌጅ። ከተመጣጣኝ ክፍልፋዮች ፣ እኩል ያልሆኑ ክፍልፋዮች ፣ የተደባለቁ ቁጥሮች ወይም የተለመዱ ክፍልፋዮች ክፍልፋዮችን እንዴት ማከል እና መቀነስ እንደሚችሉ ለማወቅ እነዚህን ደረጃዎች ይከተሉ። አንዱን መንገድ አስቀድመው ካወቁ ፣ ሌሎቹን ክፍልፋዮች መፍታት በእርግጥ ቀላል ነው!
ደረጃ
ዘዴ 1 ከ 4 - ክፍልፋዮችን ከተመሳሳይ አመላካች ጋር ማከል እና መቀነስ
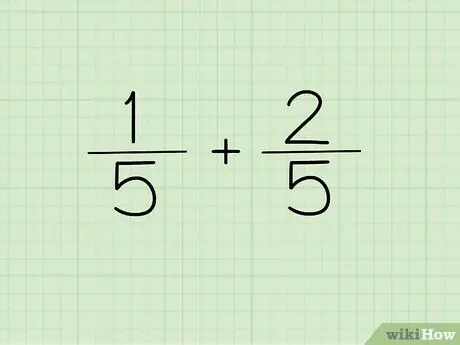
ደረጃ 1. ጥያቄዎን ይፃፉ።
ሊያክሉት ወይም ሊቀንሱት የሚፈልጉት የሁለት ክፍልፋዮች አመላካች ተመሳሳይ ከሆነ ፣ እንደ መልስዎ አመላካች አንድ ጊዜ ይፃፉ።
በሌላ አነጋገር 1/5 እና 2/5 እንደ 1/5 + 2/5 = መፃፍ የለባቸውም? ፣ ግን እንደ (1+2)/5 =?. አመላካቾች አንድ ናቸው ፣ ስለዚህ አንድ ጊዜ ብቻ ሊፃፉ ይችላሉ። ሁለቱ አሃዞች ተጣምረዋል።
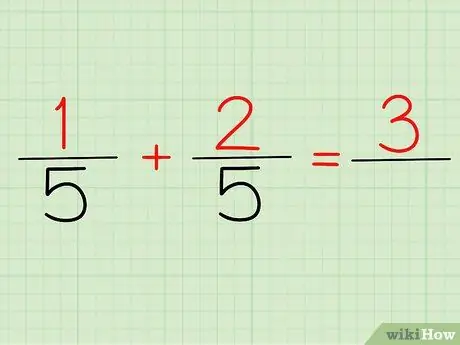
ደረጃ 2. ቁጥሮችን ይጨምሩ።
አሃዛዊው ከማንኛውም ክፍልፋይ በላይ የሆነ ቁጥር ነው። ከላይ ያለውን ችግር ከተመለከትን ፣ 1/5 እና 2/5 ፣ 1 እና 2 የእኛ አሃዞች ናቸው።
እርስዎ 1/5 + 2/5 ወይም (1 + 2)/5 ይፃፉት ፣ የእርስዎ መልስ አንድ ይሆናል 3! ምክንያቱም ፣ 1 + 2 = 3።

ደረጃ 3. አመላካችውን ይተው።
አመላካቾች አንድ ስለሆኑ ከአከፋፋዮች ጋር ምንም አታድርጉ! አትጨምር ፣ አትቀንስ ፣ አትባዛ ወይም አትከፋፈል። ይሁን በቃ.
ስለዚህ ፣ ከተመሳሳይ ምሳሌ ፣ የእኛ አመላካች 5. ትክክል ነው! 5 የእኛ ክፍልፋይ የታችኛው ቁጥር ነው። መልሱን ግማሽ አግኝተናል

ደረጃ 4. መልስዎን ይፃፉ።
አሁን ማድረግ ያለብዎ ቁጥርዎን እና አመላካችዎን መፃፍ ብቻ ነው! ከላይ ያለውን ምሳሌ ከተጠቀሙ መልስዎ 3/5 ይሆናል።
የእርስዎ ቆጣሪ ምንድን ነው? 3. መለያዎ? 5. ስለዚህ 1/5 + 2/5 ወይም (1 + 2)/5 እኩል ነው 3/5.
ዘዴ 2 ከ 4 - ክፍልፋዮችን ከተለያዩ ጠቋሚዎች ጋር ማከል እና መቀነስ

ደረጃ 1. አነስተኛውን የጋራ አመላካች ያግኙ።
ማለትም ፣ ትንሹ አመላካች ለሁለቱም ክፍልፋዮች አንድ ነው። ክፍልፋዮች 2/3 እና 3/4 አሉን እንበል። አመላካች ምንድነው? 3 እና 4. የሁለቱም ክፍልፋዮች ትንሹን የጋራ አመላካች ለማግኘት ይህንን በሦስት መንገዶች ማድረግ ይችላሉ-
- የብዙዎችን ይፃፉ። የ 3 ብዜቶች 3 ፣ 6 ፣ 9 ፣ 12 ፣ 15 ፣ 18… እና የመሳሰሉት ናቸው። የ 4 ብዜቶች? 4 ፣ 8 ፣ 12 ፣ 16 ፣ 20 ፣ ወዘተ. የሁለቱ ብዜት የሆነው ትንሹ ቁጥር ምንድነው? 12! ያ በጣም የተለመደው የጋራ መለያ ነው።
-
ጠቅላይ ፋኖቴሽን። ስለ ምክንያቶች ካወቁ ዋና ዋና የፋይናንስ መረጃን ማካሄድ ይችላሉ። ያ ማለት ፣ የእርስዎን አመላካች የሚፈጥሩትን ቁጥሮች እየፈለጉ ነው። ለቁጥር 3 ፣ ምክንያቶች 3 እና 1. ለቁጥር 4 ፣ ምክንያቶች 2 እና 2. ከዚያ ፣ ሁላችሁም። 3 x 2 x 2 = 12. አነስተኛው የጋራ መለያዎ!
ለትንሹ ቁጥር ሁሉንም ቁጥሮች ያባዙ። በአንዳንድ ችግሮች ፣ ልክ እንደዚህ ፣ ሁለቱንም ቁጥሮች ማባዛት ይችላሉ - 3 x 4 = 12. ሆኖም ፣ ትልቅ አመላካች ካለዎት ፣ ይህንን አያድርጉ! 56 x 44 ን ማባዛት እና 2,464 ን ለማግኘት ሁሉንም መውጣት አይፈልጉም

ደረጃ 2. አነስተኛውን የጋራ አመላካች ለማግኘት በሚፈለገው ቁጥር አመዳጁን ያባዙ።
በሌላ አገላለጽ ፣ የእርስዎ አመላካቾች ሁሉ እኩል እንዲሆኑ ይፈልጋሉ። በምሳሌአችን ውስጥ ፣ አመላካች 12 እንዲሆን እንፈልጋለን ፣ ከ 3 ወደ 12 ለመለወጥ ፣ 3 በ 4 እንዲባዙ ፣ 4 ን ወደ 12 ለመለወጥ ፣ 4 በ 3 እንዲባዙ 3. ተመሳሳይ አመላካች የመጨረሻ መልስዎ አመላካች ይሆናል።
-
ስለዚህ 2/3 2/3 x 4 እና 3/4 3/4 x 3. ይሆናል ፣ ማለትም አሁን 2/12 እና 3/12 አለን። ግን ፣ ገና አልጨረስንም!
- አስተናጋጆች እርስ በእርስ ሲባዙ ያስተውላሉ። ይህ በዚህ ሁኔታ ውስጥ ሊከናወን ይችላል ፣ ግን በሁሉም ሁኔታዎች ውስጥ አይደለም። አንዳንድ ጊዜ ፣ ሁለቱንም አመላካቾች ከማባዛት ይልቅ ፣ አነስተኛውን ቁጥር ለማግኘት ሁለቱንም ቁጥሮች በሌላ ቁጥር ማባዛት ይችላሉ።
- ከዚያ በሌሎች ችግሮች ውስጥ ፣ አንዳንድ ጊዜ በችግሩ ውስጥ ካለው የሌላው ክፍልፋይ እኩል እንዲሆኑ ለማድረግ አንድ አመላካች ማባዛት ብቻ ያስፈልግዎታል።

ደረጃ 3. ቁጥርን በተመሳሳይ ቁጥር ማባዛት።
አመላካችውን በቁጥር ሲያባዙ ፣ በተመሳሳይም ቁጥሩን በተመሳሳይ ቁጥር ማባዛት አለብዎት። ባለፈው ደረጃ ያደረግነው መደረግ ያለበት የማባዛት አካል ብቻ ነው።
እንደ መጀመሪያው ደረጃ 2/3x4 እና 2/4x3 አለን - ከዚያ በሁለተኛው ደረጃ 2 x 4/3 x 4 እና 3 x 3/4 x 3. ያም ማለት አዲሶቹ ቁጥራችን 8/12 እና 9/ናቸው 12. ፍጹም
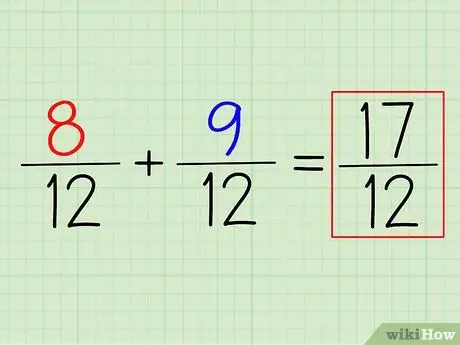
ደረጃ 4. መልሱን ለማግኘት ቁጥሮችን (ወይም መቀነስ) ይጨምሩ።
8/12 + 9/12 ን ለማከል ፣ ማድረግ የሚጠበቅብዎት የቁጥር ቁጥሮችን ማከል ብቻ ነው። ያስታውሱ - አመላካችውን ብቻ ይተው። ያገኙት ትንሹ የጋራ አመላካች የእርስዎ የመጨረሻ መለያ ነው።
በዚህ ምሳሌ ፣ (8+9)/12 = 17/12። ወደ የተቀላቀለ ቁጥር ለመለወጥ ፣ አመላካችውን ከቁጥሩ ላይ ብቻ ይቀንሱ እና ቀሪውን ይፃፉ። በዚህ ሁኔታ 17/12 = 1 5/12።
ዘዴ 3 ከ 4 - የተደባለቀ እና የተለመዱ ክፍልፋዮችን ማከል እና መቀነስ
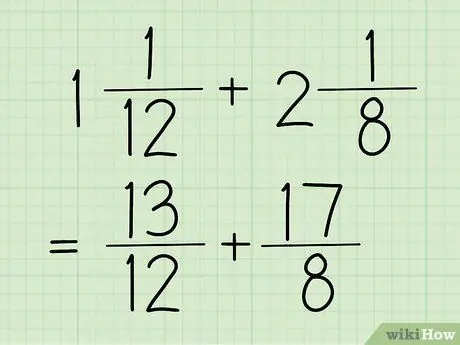
ደረጃ 1. የተደባለቀ ክፍልፋዮችዎን ወደ የተለመዱ ክፍልፋዮች ይለውጡ።
የተደባለቀ ቁጥር ከላይ በምሳሌው (1 5/12) ላይ እንዳለው ሙሉ ቁጥር እና ክፍልፋይ ያለው ክፍልፋይ ነው። ይህ በእንዲህ እንዳለ ተራ ክፍልፋይ ቁጥሩ (የላይኛው ቁጥር) ከአከፋፋይ (የታችኛው ቁጥር) የሚበልጥ ክፍል ነው። ይህ ክፍልፋይ በቀደመው ደረጃም ይታያል ፣ እሱም 17/12 ነው።
በዚህ ክፍል ላሉት ምሳሌዎች 13/12 እና 17/8 ን እንጠቀማለን።

ደረጃ 2. የጋራ አመላካች ይፈልጉ።
አነስተኛውን የጋራ አመላካች ለማግኘት ሶስቱን መንገዶች ያስታውሳሉ? ብዜቶችን በመፃፍ ፣ ዋና የፋብሪካ መረጃን በመጠቀም ወይም አመላካቾችን በማባዛት።
የእኛን ምሳሌዎች ብዛት እናገኝ ፣ 12 እና 8. ሁለቱም የሚያመሳስሏቸው ትንሹ ቁጥር ምንድነው? 24. 8 ፣ 16 ፣ 24 እና 12 ፣ 24 - ቢንጎ

ደረጃ 3. ተመጣጣኝ ክፍልፋይን ለማግኘት የእርስዎን አኃዛዊ እና አመላካች ያባዙ።
ሁለቱም ጠቋሚዎች ወደ 24 መቀየር አለባቸው። እንዴት 12 ን ወደ 24 ይቀይራሉ? በ 2. ከ 8 እስከ 24 ማባዛት? በሦስት ተባዙ። ግን አይርሱ - የቁጥር ቁጥሮችን እንዲሁ ማባዛት አለብዎት!
ስለዚህ (13 x 2)/(12 x 2) = 26/24። እና (17 x 3)/(8 x 3) = 51/24። በዚህ ልንጨርስ ተቃርበናል

ደረጃ 4. ክፍልፋዮችዎን ይጨምሩ ወይም ይቀንሱ።
አሁን አንድ ተመሳሳይ አመላካች አለዎት ፣ ሁለቱን ቁጥሮች በቀላሉ በአንድ ላይ ማከል ይችላሉ። ያስታውሱ ፣ ተከፋይውን ብቻ ይተው!
26/24 + 51/24 = 77/24። ያ የእርስዎ ድምር ነው! ሆኖም ፣ ከላይ ያሉት ቁጥሮች በጣም ትልቅ ነበሩ…

ደረጃ 5. መልስዎን ወደ ድብልቅ ቁጥሮች መልሰው ይለውጡ።
በክፍልፋይ አናት ላይ ያለው በጣም ትልቅ ቁጥር ትንሽ እንግዳ ይመስላል - የክፍልዎን መጠን መለየት አይችሉም። እርስዎ ማድረግ የሚጠበቅብዎ ሌላ ተጨማሪ መቀነስ እስካልቻለ ድረስ ቀሪውን እስከሚጽፍ ድረስ አመላካችዎን ከቁጥር ቁጥሩ ላይ በተደጋጋሚ መቀነስ ነው።
-
በዚህ ምሳሌ ፣ 77 ሲቀነስ 24 በ 3 ጊዜ። ማለትም 24 x 3 = 72. ቀሪው 5 ነው! ስለዚህ የመጨረሻ ውጤትዎ ምንድነው? 3 5/24.
እውነትም!
ዘዴ 4 ከ 4 - LCM ን ሳያገኙ ክፍልፋዮችን ይጨምሩ እና ይቀንሱ
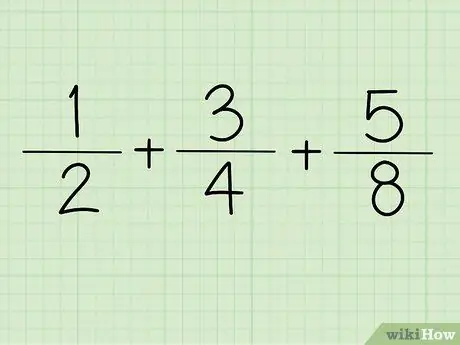
ደረጃ 1. ክፍልፋዩን ይፃፉ።
ለምሳሌ + +

ደረጃ 2. መጀመሪያ ቁጥሩን ይፍቱ።
- በሌላው ክፍልፋይ አሃዝ ያባዙ።
- 1 በ 4 እና 8. ማባዛት [32]
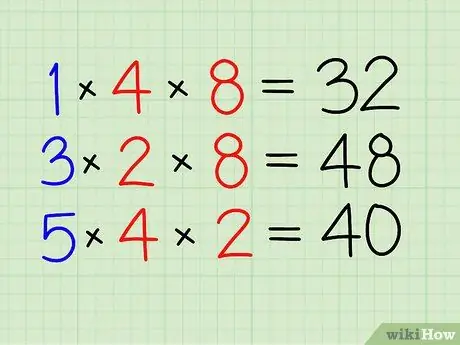
ደረጃ 3. ለሌሎቹ ክፍልፋዮች ተመሳሳይ ነገር ያድርጉ።
- 3 በ 2 እና 8. ማባዛት [48]
- በመጨረሻም 5 በ 4 እና 2. ማባዛት [40]
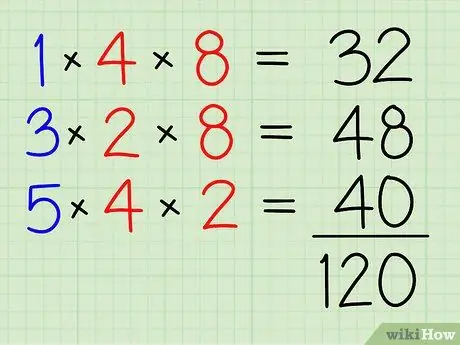
ደረጃ 4. ሁሉንም በአንድ ላይ ያክሏቸው።
32+48+40=120
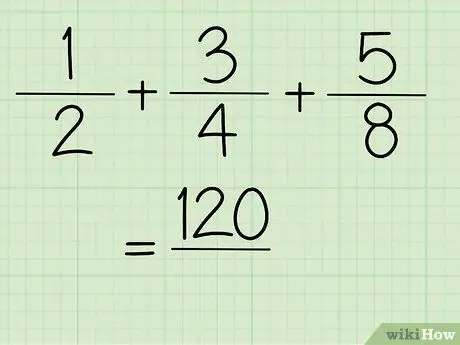
ደረጃ 5. አሁን ፣ የቁጥሩን እሴት ያገኛሉ።

ደረጃ 6. የክፍሉን አመላካች ይፍቱ።

ደረጃ 7. ሁሉንም ክፍልፋዮች አመላካቾች ያባዙ።
2×4×8=64

ደረጃ 8. አሁን ፣ ውጤቱን ያገኛሉ።
120/64 = 1 56/64 = 1 ⅞
ማስጠንቀቂያ
- ይህ ዘዴ ብዙ ቁጥሮችን ለማባዛት ያስችልዎታል።
- በዚህ መንገድ ለማስላት ካልኩሌተር ሊያስፈልግዎት ይችላል።







