አማካይ ፍጥነትን እንዴት ማስላት እንደሚቻል -12 ደረጃዎች (ከስዕሎች ጋር)

2024 ደራሲ ደራሲ: Jason Gerald | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2024-02-01 14:11

አማካይ ፍጥነቱን ለማስላት የሚያስፈልግዎት ጠቅላላ ማፈናቀል ነው። ወይም የአቀማመጥ ለውጥ ፣ እና አጠቃላይ ጊዜ። ያስታውሱ ፍጥነት እንዲሁ የነገሩን አቅጣጫ እና ፍጥነት ያሰላል ፣ ስለሆነም በመልስዎ ውስጥ እንደ “ሰሜን” ፣ “ፊት” ወይም “ግራ” ያሉ አቅጣጫን ያካትቱ። የፍጥነት ስሌት ችግርዎ የማያቋርጥ መፋጠንንም የሚያካትት ከሆነ መልሱን ይበልጥ ቀላል ለማድረግ ፈጣን መንገድን መማር ይችላሉ።

ደረጃ

ዘዴ 2 ከ 2 - የመፈናቀልን እና የጊዜን አማካይ ፍጥነት ማስላት

ደረጃ 1. ፍጥነቱ የአንድን ነገር ፍጥነት እና አቅጣጫ የሚያካትት መሆኑን ያስታውሱ።

ፍጥነት የአንድ ነገር አቀማመጥ የሚለወጥበትን ፍጥነት ይገልጻል። ይህ መደረግ ያለበት ነገሩ በምን ያህል ፍጥነት እንደሚንቀሳቀስ ብቻ ሳይሆን በእሱ አቅጣጫም ጭምር ነው። "100 ሜትር በሰከንድ ወደ ደቡብ" ከ "100 ሜትር በሰከንድ ወደ ምሥራቅ" የተለየ የፍጥነት ዋጋ ነው።

• አቅጣጫ ያላቸው መጠኖች የቬክተር መጠኖች ይባላሉ። ይህ መጠን ከተለዋዋጭው በላይ ያለውን ቀስት በመፃፍ ስካላር ብዛት ከሚባል አቅጣጫ አልባ ብዛት ሊለይ ይችላል። ለምሳሌ ፣ አጻጻፉ v ደረጃውን ይወክላል ፣ ማስታወሻው ቁ ^→ ፍጥነትን ወይም ፍጥነትን + አቅጣጫን ይወክላል። በዚህ ጽሑፍ ውስጥ ጥቅም ላይ የዋለው የ v ምልክት ፍጥነትን ይወክላል።
• በሳይንሳዊ ችግሮች ውስጥ ርቀትን ለመግለፅ ሜትሮችን ወይም ሌሎች ሜትሪክ አሃዶችን መጠቀም አለብዎት ፣ ለዕለታዊ ዓላማዎች የሚወዱትን ማንኛውንም ክፍል መጠቀም ይችላሉ።

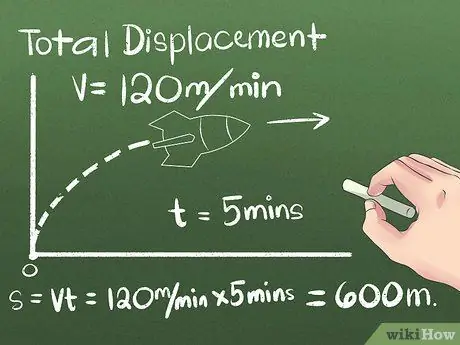
ደረጃ 2. ጠቅላላ የመፈናቀያ ዋጋን ያግኙ።

መፈናቀል ማለት የአንድ ነገር አቀማመጥ ፣ ወይም በመነሻ እና በማጠናቀቂያ ነጥቦቹ መካከል ያለው ርቀት እና አቅጣጫ ነው። በመጨረሻው ቦታ ላይ ከመድረሱ በፊት ነገሩ የሚንቀሳቀስበት አቅጣጫ ችላ ሊባል ይችላል ፣ ምክንያቱም በመነሻ እና በመጨረሻ ነጥቦች መካከል ያለው ርቀት ብቻ ግምት ውስጥ ይገባል። ለመጀመሪያው ምሳሌ ፣ በአንድ አቅጣጫ በቋሚ ፍጥነት የሚንቀሳቀስን ነገር እንጠቀማለን-

• አንድ ሮኬት በደቂቃ 120 ሜትር በቋሚ ፍጥነት ለ 5 ደቂቃዎች ወደ ሰሜን እየሄደ ነው ይበሉ። የመጨረሻውን ቦታ ለማስላት ቀመሩን s = vt ይጠቀሙ ወይም ከዚያ በኋላ (5 ደቂቃዎች) (120 ሜትር/ደቂቃ) = በሮኬቱ የተጓዘውን ርቀት ለማስላት ተግባራዊ አስተሳሰብን ይጠቀሙ። 600 ሜትር ሰሜን ከመነሻ ነጥብ።
• የማያቋርጥ ማፋጠን ለሚከሰቱ ችግሮች በ s = vt + at እነሱን መፍታት ይችላሉ²፣ ወይም መልሱን ለማግኘት በሌላ ክፍል የተገለጸውን አጭር ዘዴ ይጠቀሙ።

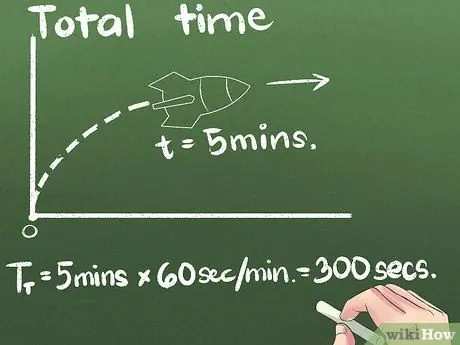
ደረጃ 3. ያጠፋውን ጠቅላላ ጊዜ ይፈልጉ።

በእኛ ምሳሌ ውስጥ ሮኬቱ ለ 5 ደቂቃዎች ወደፊት ይራመዳል። በማንኛውም የጊዜ አሃድ ውስጥ አማካይ ፍጥነቱን መግለፅ ይችላሉ ፣ ሁለተኛው ግን ዓለም አቀፍ የሳይንስ መደበኛ አሃድ ነው። በዚህ ምሳሌ ውስጥ የሰከንዶች አሃዶችን እንለውጣለን ((5 ደቂቃዎች) x (60 ሰከንዶች/ደቂቃ) = 300 ሰከንዶች.

በሳይንሳዊ ችግሮች ውስጥ እንኳን ፣ ጥያቄው ሰዓቱን ወይም ትልቁን የጊዜ አሃድ የሚጠቀም ከሆነ ፣ መጀመሪያ ፍጥነቱን ለማስላት ቀላል ይሆናል ፣ ከዚያ የመጨረሻውን መልስ ወደ ሜትር/ሰከንድ ይለውጡ።

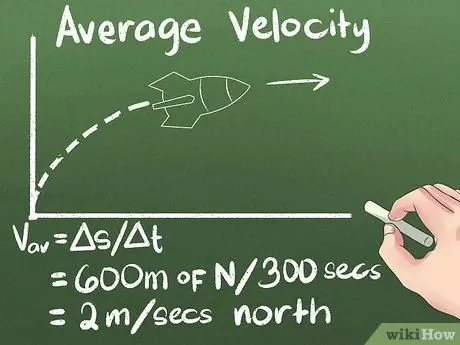
ደረጃ 4. አማካይ ፍጥነቱን በጊዜ እንደ መፈናቀል ያሰሉ።

አንድ ነገር ምን ያህል እንደሚንቀሳቀስ ፣ እና እዚያ ለመድረስ ምን ያህል ጊዜ እንደሚወስድ ካወቁ ፣ ምን ያህል በፍጥነት እንደሚንቀሳቀስ ያውቃሉ። ስለዚህ እኛ ለምንጠቀምበት ምሳሌ የሮኬቱ አማካይ ፍጥነት (600 ሜትር ሰሜን) / (300 ሰከንዶች) = ነው 2 ሜትር/ሰሜን ሰሜን.

• መመሪያን (እንደ “ፊት” ወይም “ሰሜን”) ማካተትዎን ያስታውሱ።
• በቀመር ውስጥ ቁ_አ = ሰ/Δt. የዴልታ ምልክት “ለውጥ” ማለት ነው ፣ ስለዚህ s/Δt ማለት “በተወሰነ ጊዜ ውስጥ የአቀማመጥ ለውጥ” ማለት ነው።
• አማካይ ፍጥነት እንደ ቁ ሊጻፍ ይችላል_አ, ወይም ከላይ እንደ አግዳሚ መስመር ያለው ቁ.

ደረጃ 5. ይበልጥ የተወሳሰቡ ችግሮችን ይፍቱ።

አንድ ነገር አቅጣጫውን ወይም ፍጥነቱን ከቀየረ ፣ ግራ አትጋቡ። አማካይ ፍጥነት አሁንም ከጠቅላላው መፈናቀል እና ከጠቅላላው ጊዜ “ብቻ” ይሰላል። ችላ ሊሉት በሚችሉት የመጀመሪያ እና መጨረሻ ነጥቦች መካከል ምን ይከሰታል። ከተመሳሳይ መፈናቀል እና አጠቃላይ ጊዜ ጋር የሚጓዝ አንድ ነገር የሚከተሉት ምሳሌዎች ናቸው ፣ እና ስለዚህ ፣ ተመሳሳይ አማካይ ፍጥነት

• አና በምዕራብ በ 1 ሜትር/ሰከንድ ለ 2 ሰከንዶች ትሄዳለች ፣ ከዚያም በድንገት ወደ 3 ሜትር/ሰከንድ በፍጥነት ትሄዳለች እና ለ 2 ሰከንዶች ወደ ምዕራብ መሄዷን ትቀጥላለች። ጠቅላላው መፈናቀል (1 ሜ/ሰ ወደ ምዕራብ) (2 ሴኮንድ) + (3 ሜ/ሰ ምዕራብ) (2 ሴኮንድ) = 8 ሜትር ወደ ምዕራብ። ጠቅላላው ጊዜ 2 ሰከንዶች + 2 ሰከንዶች = 4 ሰከንዶች ነው። ስለዚህ አማካይ ፍጥነት 8 ሜትር ምዕራብ/ 4 ሰከንዶች = ነው 2 ሜትር/ሰከንድ ምዕራብ።

• ባርት ወደ ምዕራብ በ 5 ሜትር/ሰከንድ ለ 3 ሰከንዶች ይራመዳል ፣ ከዚያ ዞሮ በ 7 ሜትር/ሰከንድ ለ 1 ሰከንድ ይራመዳል። የምስራቃዊውን እንቅስቃሴ እንደ “አሉታዊ የምዕራብ እንቅስቃሴ” አድርገን ልናስብ እንችላለን ስለዚህ አጠቃላይ መፈናቀሉ = (5 ሜትር/ሰከንድ ወደ ምዕራብ) (3 ሴኮንድ) + (-7 ሜ/ሰ ምዕራብ) (1 ሴኮንድ) = 8 ሜትር ነው። ጠቅላላ ጊዜ = 4 ሰከንዶች። አማካይ ፍጥነት = 8 ሜትር ምዕራብ / 4 ሰከንዶች = 2 ሜትር/ሰከንድ ምዕራብ።

• ሻርሎት በሰሜን 1 ሜትር ተጓዘች ከዚያም ወደ ምዕራብ 8 ሜትር ፣ ከዚያም ደቡብ 1 ሜትር ተጓዘች። ጉዞውን በሙሉ ለማጠናቀቅ የሚወስደው ጊዜ 4 ሰከንዶች ነው። በወረቀት ላይ ንድፉን ይሳሉ ፣ እና የመጨረሻው ነጥብ ከመነሻው ነጥብ በስተ ምዕራብ 8 ሜትር ነው ፣ ስለዚህ ይህ እሴት መፈናቀል ነው። የሚወስደው ጠቅላላ ጊዜ 4 ሰከንዶች ነው ፣ ስለዚህ አማካይ ፍጥነት 8 ሜትር ምዕራብ / 4 ሰከንዶች = ነው 2 ሜትር/ሰከንድ ምዕራብ።

  ዘዴ 2 ከ 2 - የቋሚ ፍጥነቱን አማካይ ፍጥነት ማስላት

  

  ደረጃ 1. የመጀመሪያውን ፍጥነት እና የማያቋርጥ ፍጥነትን ያስቡ።

  እንበል ችግራችን “ብስክሌት በ 5 ሜ/ሰ ፍጥነት ፣ በ 2 ሜ/ሰ የማያቋርጥ ፍጥነት ወደ ቀኝ እየሄደ ነው።². ይህ ብስክሌት ለ 5 ሰከንዶች የሚንቀሳቀስ ከሆነ አማካይ ፍጥነቱ ምንድነው?”

  ክፍሉ “ሜትር/ሰከንድ ከሆነ²እርስዎን ለማደናገር ፣ እንደ “ሜትር/ሰከንድ/ሰከንድ” ወይም “ሜትር በሰከንድ” ብለው ይፃፉ። 2 ሜትር/ሰከንድ/ሰከንድ ማፋጠን ማለት ፍጥነቱ በየሴኮንድ በ 2 ሜትር በሰከንድ እየጨመረ ነው ማለት ነው።

  

  ደረጃ 2. የመጨረሻውን ፍጥነት ለማግኘት ፍጥነትን ይጠቀሙ።

  በማስታወቂያው ሀ የተጠቀሰው ማፋጠን የፍጥነት (ወይም ተመን) የለውጥ መጠን ነው። ፍጥነት በቋሚ ጭማሪ ፍጥነት ይጨምራል። በብስክሌት ጉዞው ውስጥ በተለያዩ ጊዜያት ፍጥነቱን ለማግኘት ፍጥነትን በመጠቀም ጠረጴዛን መሳል ይችላሉ። የችግሩን የመጨረሻ ነጥብ (በ t = 5 ሰከንዶች) ለማግኘት ይህንን ሰንጠረዥ መፍጠር አለብን ፣ ግን ይህንን ፅንሰ -ሀሳብ በቀላሉ እንዲረዱዎት ለማድረግ ረዘም ያለ ጠረጴዛ እንፈጥራለን-

  • በመነሻ ነጥብ (ጊዜ t = 0 ሰከንዶች) ፣ ብስክሌቱ በ 5 ሜትር/ሰ ፍጥነት እየተጓዘ ነው።
  • ከ 1 ሰከንድ (t = 1) በኋላ ብስክሌቱ በ 5 ሜትር/ሰከንድ + በ = 5 ሜትር/ሰከንድ + (2 ሜትር/ሰከንድ)²) (1 ሰከንድ) = 7 ሜትር/ሰከንድ።
  • በ t = 2 ፣ ብስክሌቱ በ 5+ (2) (2) = 9 ሜትር/ሰከንድ ፍጥነት ወደ ቀኝ ይንቀሳቀሳል።
  • በ t = 3 ፣ ብስክሌቱ በ 5+ (2) (3) = 11 ሜትር/ሰከንድ ፍጥነት ወደ ቀኝ ይንቀሳቀሳል።
  • በ t = 4 ፣ ብስክሌቱ በ 5+ (2) (4) = 13 ሜትር/ሰከንድ ፍጥነት ወደ ቀኝ ይንቀሳቀሳል።
  • በ t = 5 ፣ ብስክሌቱ በ 5+ (2) (5) = ፍጥነት ወደ ቀኝ ይንቀሳቀሳል 15 ሜትር/ሰከንድ.

  

  ደረጃ 3. አማካይ ፍጥነቱን ለማግኘት ይህንን ቀመር ይጠቀሙ።

  ፍጥነቱ የማያቋርጥ ከሆነ እና “ብቻ” ፣ አማካይ ፍጥነቱ ከመጨረሻው እና ከመጀመሪያው ፍጥነቶች ድምር አማካይ እሴት ጋር እኩል ይሆናል። (ቁ_ረ +ቁ_እኔ)/2. ከላይ ላለው የእኛ ምሳሌ ችግር ፣ የብስክሌቱ የመጀመሪያ ፍጥነት ቁ_እኔ 5 ሜትር/ሰከንድ። እኛ ካሰላን በኋላ የመጨረሻው ፍጥነት ቁ_ረ 15 ሜትር/ሰከንድ። እነዚህን ሁለት እሴቶች አንድ ላይ በማከል (15 ሜትር/ሰከንድ + 5 ሜትር/ሰከንድ)/2 = (20 ሜትር/ሰከንድ)/2 = 10 ሜትር/ሰከንድ ትክክለኛ አቅጣጫ.

  • በዚህ ጉዳይ ላይ “ትክክል” የሚለውን አቅጣጫ ማካተትዎን ያስታውሱ።
  • ይህ ቃል እንደ ቁ ሊጻፍ ይችላል₀ (ፍጥነት በ 0 ፣ ወይም የመጀመሪያ ፍጥነት) እና v (የመጨረሻ ፍጥነት)።

  

  ደረጃ 4. የአማካይ የፍጥነት ቀመርን በስሜታዊነት ይረዱ።

  አማካይ ፍጥነቱን ለማግኘት ፣ ፍጥነቱን በማንኛውም ነጥብ መጠቀም እና ለሁሉም አማካይ ማግኘት እንችላለን። (ይህ የአማካይ ፍቺ ነው።) ይህ ስሌት ወይም ማለቂያ የሌለው ጊዜን የሚፈልግ በመሆኑ ይህንን ቀመር በበለጠ ለመረዳት ይረዱ። እያንዳንዱን ጊዜ ከመውሰድ ይልቅ የሁለቱ የጊዜ ነጥቦችን አማካይ ፍጥነት ያሰሉ እና ውጤቱን ይመልከቱ። በጊዜ ውስጥ አንድ ነጥብ ብስክሌቱ በዝግታ የሚሄድበት ጉዞው መጀመሪያ ላይ ነው ፣ እና ሌላኛው ነጥብ ብስክሌቱ በፍጥነት የሚሄድበት የመጨረሻ ነጥብ አጠገብ ነው።

  

  ደረጃ 5. ሊሞክር የሚችል ጽንሰ -ሀሳብን ይፈትሹ።

  በሰዓቱ በተለያዩ ነጥቦች ላይ ፍጥነቱን ለመወሰን ከላይ ያለውን ሰንጠረዥ ይጠቀሙ። የእኛን መስፈርት የሚያሟሉ አንዳንድ ጥንዶች (t = 0 ፣ t = 5) ፣ (t = 1 ፣ t = 4) ፣ ወይም (t = 2 ፣ t = 3)። ከፈለጉ ፣ ይህንን ቀመር ከቲቲጀሮች በተጨማሪ ከሌሎች እሴቶች ጋር መሞከር ይችላሉ።

  የትኛውን ጥንድ ነጥቦች ቢመርጡ ፣ በዚያን ጊዜ አማካይ ፍጥነት ሁል ጊዜ ተመሳሳይ ይሆናል። ለምሳሌ ፣ ((5+15)/2) ፣ ((7+13)/2) ፣ ወይም ((9+11)/2) ሁሉም በቀኝ 10 ሜትር/ሰከንድ እኩል ናቸው።

  

  ደረጃ 6. የሚታወቅ ማብራሪያውን ይሙሉ።

  እኛ በተወሰነው እያንዳንዱ ጊዜ ዝርዝር ይህንን ዘዴ ከተጠቀምን ፣ የጉዞውን የመጀመሪያ አጋማሽ እና የጉዞውን ሁለተኛ አጋማሽ አማካይ ማስላት እንቀጥላለን። እያንዳንዱን ግማሽ ለመሸፈን የሚወስደው ጊዜ አንድ ነው ፣ ስለዚህ ቆጠራውን ስንጨርስ ምንም ፍጥነት አይጠፋም።

  • ሁለቱም ጥንድ ተመሳሳይ ውጤት ስለሚሰጡ ፣ የእነዚህ ፍጥነቶች አማካይ እንዲሁ በእሴት ተመሳሳይ ይሆናል። በእኛ ምሳሌ ፣ የጠቅላላው ፍጥነት “10 ሜትር/ሰከንድ ወደ ቀኝ” አሁንም 10 ሜትር/ሰከንድ ይሆናል።
  • የማንኛውንም ጥንድ አማካይ ፣ ለምሳሌ የመጀመሪያ እና የመጨረሻ ፍጥነቶችን በማስላት ይህንን እሴት ማግኘት እንችላለን። በእኛ ምሳሌ እነዚህ ፍጥነቶች በ t = 0 እና t = 5 ላይ ደርሰዋል ፣ እና ከላይ ያለውን ቀመር በመጠቀም (5+15)/2 = 10 ሜትር/ሰከንድ በቀኝ በኩል ሊሰሉ ይችላሉ።

  

  ደረጃ 7. ይህንን ቀመር በሂሳብ ይረዱ።

  እንደ ቀመሮች በተፃፉ ማስረጃዎች የበለጠ ምቾት የሚሰማዎት ከሆነ ፣ የማያቋርጥ ፍጥነቱን ግምት ውስጥ በማስገባት የተጓዘውን ርቀት ለማስላት ቀመር መጀመር እና ቀመርውን ከዚያ ማግኘት ይችላሉ-

  • s = v_እኔt + በ². (በቴክኒካዊ s እና t ፣ ወይም በአቀማመጥ ይለውጡ እና በጊዜ ይለወጣሉ ፣ ግን እርስዎ እና እርስዎ ቢጽፉ እርስዎም እንዲሁ ይረዱዎታል።)
  • አማካይ ፍጥነት v_አ s/t ተብሎ ይገለጻል ፣ ስለዚህ ቀመሩን በ s/t መልክ ያስገቡ።
  • ቁ_አ = s/t = v_እኔ + በ
  • የፍጥነት x ጊዜ በጠቅላላው የፍጥነት ለውጥ ወይም ቁ ጋር እኩል ነው_ረ - ቁ_እኔ. ስለዚህ በቀመር ውስጥ “በ” ን መተካት እና ማግኘት እንችላለን-
  • ቁ_አ = ቁ_እኔ + (ቁ_ረ - ቁ_እኔ).
  • ቀለል ያድርጉት - v_አ = ቁ_እኔ + ቁ_ረ - ቁ_እኔ = ቁ_እኔ + ቁ_ረ = (ቁ_ረ +ቁ_እኔ)/2.

  ጠቃሚ ምክሮች

  • ፍጥነቱ ከፍጥነት የተለየ ነው ምክንያቱም ፍጥነቱ የቬክተር ብዛት ሲሆን ፍጥነቱ ግን ስካላር መጠን ነው። የቬክተር መጠኖች አቅጣጫውን እና መጠኑን ያካተተ ሲሆን ፣ መጠነ -ሰፊ መጠኖች ግን መጠነ -ሰፊን ብቻ ያካትታሉ።
  • ነገሩ በአንድ ልኬት የሚንቀሳቀስ ከሆነ ፣ ለምሳሌ ፣ ግራ-ቀኝ ፣ አንድ አቅጣጫን (እንደ ቀኝ) እና ሌላ አቅጣጫን (ግራ) ለመወከል አሉታዊ ቁጥርን መጠቀም ይችላሉ። ስራዎን ለሚያነቡ ሰዎች ግልፅ እንዲሆን ይህንን ማስታወሻ በገጽዎ አናት ላይ ይፃፉ።