IQR ን ለመወሰን 3 መንገዶች

2024 ደራሲ ደራሲ: Jason Gerald | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2023-12-16 10:52

IQR የውሂብ ስብስብ ውስጠ -ወሰን ክልል ወይም የአራተኛው ሥር ክልል ነው። IQR ስለ የውሂብ ስብስብ መደምደሚያዎችን ለማገዝ በስታቲስቲክ ትንታኔ ውስጥ ጥቅም ላይ ይውላል። IQR ከክልል በላይ ብዙ ጊዜ ጥቅም ላይ ይውላል ፣ ምክንያቱም IQR የውጭውን መረጃ አያካትትም። IQR ን እንዴት ማግኘት እንደሚችሉ ለማወቅ ማንበብ ይቀጥሉ!

ደረጃ

ዘዴ 1 ከ 3 - IQR ን መረዳት

ደረጃ 1. IQR ን እንዴት እንደሚጠቀሙ ይረዱ።

በመሠረቱ ፣ IQR የቁጥሮች ስብስብ ስርጭትን የመረዳት መንገድ ነው። የስር ቋት ክልል በውሂብ ስብስብ የላይኛው ቋት (25% ከላይ) እና በታችኛው ቋት (25% ዝቅተኛው) መካከል ያለው ልዩነት ነው።

ጠቃሚ ምክር

የታችኛው ቋት ብዙውን ጊዜ እንደ Q1 ይፃፋል ፣ እና የላይኛው ቋት እንደ Q3 ይፃፋል - ይህም በቴክኒካዊ የመረጃው መካከለኛ ነጥብ Q2 እና ከፍተኛው ነጥብ Q4 እንዲሆን ያደርገዋል።

ደረጃ 2. ጭቅጭቁን ይረዱ።

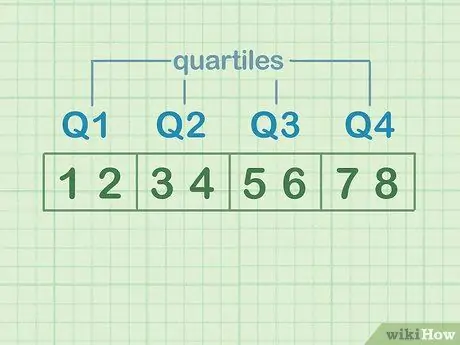
ጠብ ለማብራራት የቁጥሮችን ስብስብ በአራት እኩል ክፍሎች ይከፋፍሉ። እያንዳንዳቸው እነዚህ ክፍሎች “ጠብ” ናቸው። የመረጃ ስብስቦቹ 1 ፣ 2 ፣ 3 ፣ 4 ፣ 5 ፣ 6 ፣ 7 ፣ 8 ናቸው እንበል።

1 እና 2 የመጀመሪያው አራተኛ ወይም ጥ 1 ናቸው
3 እና 4 ሁለተኛው አራተኛ ወይም ጥ 2 ናቸው
5 እና 6 ሦስተኛው አራተኛ ወይም ጥ 3 ናቸው
7 እና 8 አራተኛው አራተኛ ወይም ጥ 4 ናቸው

ደረጃ 3. ቀመሩን ይማሩ።

በላይኛው እና በታችኛው ሩብ መካከል ያለውን ልዩነት ለማግኘት 75 ኛውን መቶኛ ከ 25 ኛው መቶኛ መቀነስ አለብዎት።

ቀመር የተፃፈው - Q3 - Q1 = IQR።

ዘዴ 2 ከ 3 - የውሂብ ስብስቡን ማጠናቀር

ደረጃ 1. ውሂብዎን ይሰብስቡ።

IQR ን በክፍል ውስጥ እና በፈተናዎች ውስጥ ካጠኑ ፣ አስቀድሞ የተዘጋጀ የውሂብ ስብስብ ሊሰጥዎት ይችላል ፣ ለምሳሌ 1 ፣ 4 ፣ 5 ፣ 7 ፣ 10. ይህ የእርስዎ የውሂብ ስብስብ ነው - አብረው የሚሰሩዋቸው ቁጥሮች። ሆኖም ፣ ከሠንጠረዥ ጥያቄዎች ወይም ከታሪክ ችግሮች የራስዎን ቁጥሮች መገንባት ይችላሉ።

እያንዳንዱ ቁጥር አንድን ነገር የሚወክል መሆኑን ያረጋግጡ ፦

ለምሳሌ ፣ በተወሰነው የአእዋፍ ብዛት በእያንዳንዱ ጎጆ ውስጥ የእንቁላል ብዛት ፣ ወይም በአንድ የተወሰነ ብሎክ ውስጥ በእያንዳንዱ ቤት ውስጥ የሚገኙ የመኪና ማቆሚያ ቦታዎች ብዛት።

ደረጃ 2. ውሂብዎን ከፍ ባለ ቅደም ተከተል ደርድር።

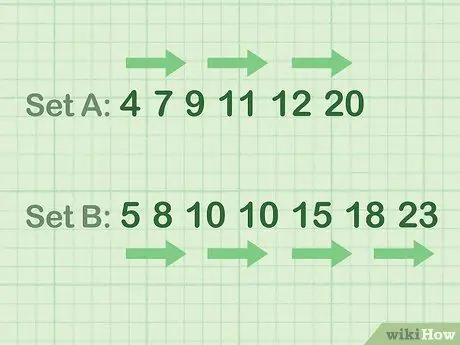
በሌላ አገላለጽ ቁጥሮቹን ከትንሽ እስከ ትልቁ ያዘጋጁ። ከሚከተሉት ምሳሌዎች ፍንጮችን ይጠቀሙ።

የቁጥር ውሂብ እንኳን ምሳሌ (አዘጋጅ ሀ) 4 7 9 11 12 20
ያልተለመደ የቁጥር ውሂብ ምሳሌ (አዘጋጅ ለ) 5 8 10 10 15 18 23 23

ደረጃ 3. ውሂቡን በሁለት ይከፋፍሉት።

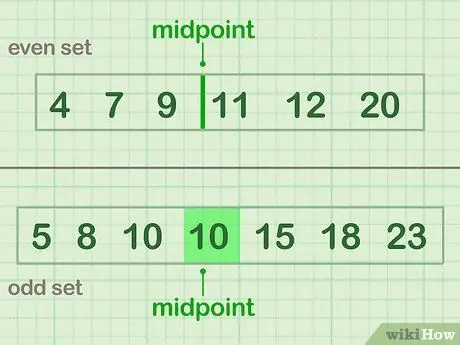
በግማሽ ለመከፋፈል ፣ የውሂብዎን መካከለኛ ነጥብ ይፈልጉ - በውሂብ ስብስብ መሃል ላይ ያለው ቁጥር ወይም ቁጥሮች። ያልተለመደ የውሂብ ቁጥር ካለዎት በመሃል ላይ ያለውን ትክክለኛውን ቁጥር ይምረጡ። እኩል የሆነ የውሂብ ቁጥር ካለዎት ፣ መካከለኛው ነጥብ በሁለቱ በጣም መካከለኛ ቁጥሮች መካከል ነው።

በ 9 እና 11: 4 7 9 መካከል መካከለኛ ነጥብ ያለው እኩል ምሳሌ (አዘጋጅ ሀ) 11 12 20
የእሴት (10): 5 8 10 (10) 15 18 23 የሆነ መካከለኛ ምሳሌ (Set B)

ዘዴ 3 ከ 3 - IQR ን ማስላት

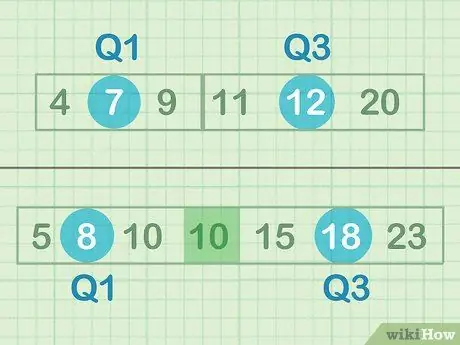
ደረጃ 1. የውሂብዎን የታችኛው እና የላይኛውን ግማሽ መካከለኛ ያግኙ።

ሚዲያን በቁጥሮች ስብስብ መሃል ላይ ያለው “መካከለኛ ነጥብ” ወይም ቁጥር ነው። በዚህ ሁኔታ ፣ የሁሉም ቁጥሮች መካከለኛ ነጥብን እየፈለጉ አይደለም ፣ ነገር ግን የላይኛውን እና የታችኛው የውሂብ ንዑስ ንፅፅሮችን አንጻራዊ መካከለኛ ነጥብ ይፈልጋሉ። ያልተለመደ የውሂብ ቁጥር ካለዎት የመካከለኛውን ቁጥር አያካትቱ - ለምሳሌ ፣ በ Set B ውስጥ ፣ አንድ ነጠላ 10 ማካተት አያስፈልግዎትም።

ምሳሌ እንኳን (ሀ አዘጋጅ)
- የመረጃው የታችኛው ግማሽ መካከለኛ = 7 (Q1)
- የውሂብ የላይኛው ግማሽ መካከለኛ = 12 (Q3)
እንግዳ ምሳሌ (ለ ለ)
- የመረጃው የታችኛው ግማሽ መካከለኛ = 8 (Q1)
- የውሂብ የላይኛው ግማሽ መካከለኛ = 18 (Q3)

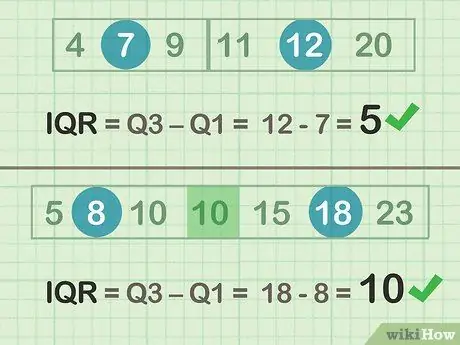
ደረጃ 2. IQR ን ለመወሰን Q3-Q1 ን ይቀንሱ።

አሁን በ 25 ኛው እና በ 75 ኛው መቶኛ መካከል ስንት ቁጥሮች እንደሚወድቁ ያውቃሉ። የውሂብ ስርጭትን ለመረዳት ይህንን ቁጥር መጠቀም ይችላሉ። ለምሳሌ ፣ አንድ ፈተና ከፍተኛው ውጤት 100 ከሆነ ፣ እና የውጤቱ IQR 5 ከሆነ ፣ የከፍተኛ እና ዝቅታዎች ክልል በጣም ትልቅ ስላልሆነ ፈተናውን የሚወስዱ አብዛኞቹ ሰዎች ተመሳሳይ ግንዛቤ አላቸው ማለት ይችላሉ። ሆኖም ፣ የፈተና ውጤት IQR 30 ከሆነ ፣ አንዳንድ ሰዎች ለምን ከፍተኛ ውጤት ሲያመጡ ሌሎቹ ደግሞ በጣም ዝቅተኛ ውጤት እንዳላቸው ማሰብ ሊጀምሩ ይችላሉ።