የሌንስ ማጉላትን እንዴት ማስላት እንደሚቻል -12 ደረጃዎች (ከስዕሎች ጋር)

2024 ደራሲ ደራሲ: Jason Gerald | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2024-01-16 19:06

የኦፕቲካል መሣሪያዎችን በማጥናት ፣ የሌንስ መሰል ነገር “ማጉላት” የሚያዩት የምስል ቁመት ከእውነተኛው ትክክለኛ ቁመት ጋር ነው። ለምሳሌ ፣ አንድን ነገር በጣም ትልቅ እንዲመስል ሊያደርግ የሚችል ሌንስ ‹ከፍተኛ› የማጉላት ምክንያት አለው ፣ አንድን ነገር ትንሽ እንዲመስል የሚያደርግ ሌንስ ‹ዝቅተኛ› የማጉላት ምክንያት አለው። የአንድን ነገር የማስፋት ቀመር ብዙውን ጊዜ ቀመር በመጠቀም ይሰላል መ = (ሸ_እኔ/ሰ_o) = -(መ_እኔ/መ_o) ፣ M = ማጉላት ፣ ሸ_እኔ = የምስል ቁመት ፣ ሸ_o = የነገር ቁመት ፣ እና መ_እኔ እና ዲ_o = የምስል እና የነገር ርቀት።

ደረጃ

ዘዴ 1 ከ 2 - ነጠላ ሌንስ ማጉላት ማስላት

ማስታወሻዎች ሀ የሚገጣጠም ሌንስ ከጠርዙ (ከማጉያ መስታወት) ይልቅ በማዕከሉ ውስጥ ሰፊ። ሀ የተለየ ሌንስ ከማዕከሉ (እንደ ጎድጓዳ ሳህን) ይልቅ ጠርዝ ላይ ሰፊ። በሁለቱም ሌንሶች ላይ ያለውን ማጉላት ማስላት አንድ ነው ፣ ጋር አንድ አስፈላጊ ልዩነት. ወደ ተለዩ ሌንሶች በቀጥታ ወደ ልዩ ሁኔታዎች ለመሄድ እዚህ ጠቅ ያድርጉ።

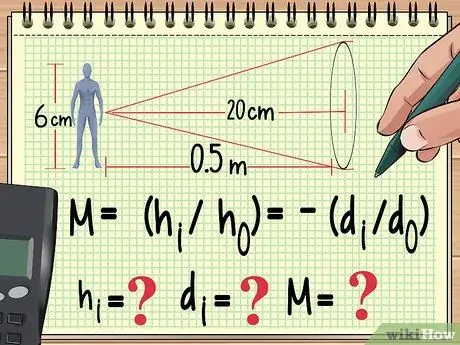
ደረጃ 1. በእርስዎ ቀመር እና አስቀድመው በሚያውቋቸው ተለዋጮች ይጀምሩ።

ልክ እንደማንኛውም የፊዚክስ ችግር ፣ የማስፋፊያ ችግርን ለመፍታት የሚቻልበት መንገድ እሱን ለማስላት የሚጠቀሙበት ቀመር መፃፍ ነው። ከዚህ ሆነው ፣ እርስዎ ከሚጠቀሙበት ቀመር ያላገኙትን ተለዋዋጭ እሴት ለማግኘት ወደ ኋላ መስራት ይችላሉ።

• ለምሳሌ ፣ 6 ሴንቲ ሜትር ቁመት ያለው አሻንጉሊት አንድ ሜትር ከ ሀ ተቀመጠ እንበል የሚገጣጠም ሌንስ በ 20 ሴ.ሜ የትኩረት ርዝመት። የማጉላት ፣ የምስል ቁመት እና የምስል ርቀትን ለማስላት ከፈለግን የእኛን ቀመር እንደሚከተለው መጻፍ መጀመር እንችላለን-

  መ = (ሸ_እኔ/ሰ_o) = -(መ_እኔ/መ_o)

• አሁን ኤች_o (የአሻንጉሊት ቁመት) እና መ_o (የአሻንጉሊት ርቀት ከሌንስ)። እንዲሁም በዚህ ቀመር ውስጥ የሌለውን የሌንስ የትኩረት ርዝመት እናውቃለን። እንቆጥራለን ሸ_እኔ፣ መ_እኔ፣ እና ኤም.

ደረጃ 2. ለማግኘት የሌንስ ቀመር በመጠቀም መ_እኔ.

እርስዎ ከሚያጉሉት ነገር ርቀቱን እና የሌንስን የትኩረት ርዝመት ካወቁ ፣ ከተሰራው ምስል ርቀትን ማስላት በሌንስ ቀመር በጣም ቀላል ነው። የሌንስ ቀመር እኩል ነው 1/f = 1/መ_o + 1/መ_እኔ ፣ f = የትኩረት ርዝመት ሌንስ።

• በዚህ ምሳሌ ችግር ውስጥ ፣ ለመቁጠር የሌንስ ቀመርን መጠቀም እንችላለን_እኔ. የ f እና d እሴቶችን ያስገቡ_እኔ ከዚያ እኩልታውን ይፍቱ

  1/f = 1/መ_o + 1/መ_እኔ

  1/20 = 1/50 + 1/መ_እኔ

  5/100 - 2/100 = 1/መ_እኔ

  3/100 = 1/መ_እኔ

  100/3 = መ_እኔ = 33.3 ሴ.ሜ

• የሌንስ የትኩረት ርዝመት ከሌንስ መሃል ወደ ብርሃን በትኩረት ነጥብ ወደሚተላለፍበት ርቀት ነው። በሚቃጠሉ ጉንዳኖች ላይ ብርሃንን በአጉሊ መነጽር ካተኮሩ ፣ አይተውታል። በትምህርቱ ውስጥ ባሉት ጥያቄዎች ውስጥ ፣ ብዙውን ጊዜ የዚህ ነጥብ ነጥብ መጠን ተሰጥቷል። በእውነተኛ ህይወት ፣ እነዚህ መመዘኛዎች ብዙውን ጊዜ ሌንስ ላይ በሚገኝ መለያ ላይ ይፃፋሉ።

ደረጃ 3. ማስላት ሸ_እኔ.

እርስዎ ካሰሉ በኋላ መ_o እና ዲ_እኔ, የተጎላውን ነገር ቁመት እና የሌንስን ማጉላት ማስላት ይችላሉ። በሌንስ ማጉላት እኩልታ ውስጥ ሁለቱ እኩል ምልክቶች (M = (ሸ_እኔ/ሰ_o) = -(መ_እኔ/መ_o)) - ይህ ማለት ሁሉም የዚህ ቀመር ክፍሎች እርስ በእርስ እኩል ናቸው ፣ ስለሆነም M እና h ን ማስላት እንችላለን_እኔ በፈለግነው ቅደም ተከተል።

• ለዚህ ምሳሌ ችግር ሸን ማስላት እንችላለን_እኔ ልክ እንደዚህ:

  (ሸ_እኔ/ሰ_o) = -(መ_እኔ/መ_o)

  (ሸ_እኔ/6) = -(33, 3/50)

  ሸ_እኔ = -(33, 3/50) x 6

  ሸ_እኔ = - 3 ፣ 996 ሳ.ሜ

• እዚህ ያለው የነገር ቁመት አሉታዊ መሆኑን ልብ ይበሉ ፣ ይህም በኋላ የምናየው ምስል የተገላቢጦሽ (ከላይ-ታች) ይሆናል።

ደረጃ 4. ኤም

የመጨረሻውን ተለዋዋጭ በቀመር ማስላት ይችላሉ -(መ_እኔ/መ_o) ወይም (ሸ_እኔ/ሰ_o).

• በሚከተለው ምሳሌ ውስጥ M ን እንዴት ማስላት እንደሚቻል እንደሚከተለው ነው

  መ = (ሸ_እኔ/ሰ_o)

  መ = (-3 ፣ 996/6) = - 0, 666

• የ d ዋጋን በመጠቀም ሲሰላ ውጤቱ እንዲሁ ይሆናል

  መ = -(መ_እኔ/መ_o)

  መ = -(33 ፣ 3/50) = - 0, 666

• አጉላ አሃድ መለያ ምልክት እንደሌለው ልብ ይበሉ።

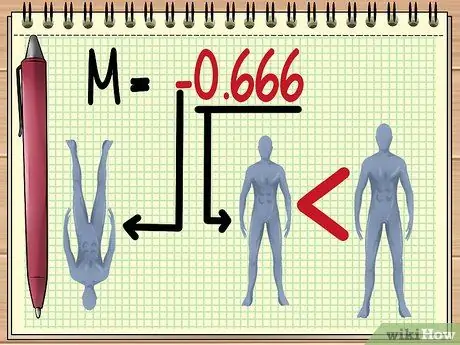
ደረጃ 5. የ M ዋጋን መረዳት።

አንዴ የ M እሴትን መጠን ካገኙ ፣ በሌንስ በኩል ስለሚያዩት ምስል ብዙ ነገሮችን መገመት ይችላሉ ፣

• መጠኑ.

  የ M “ፍፁም እሴት” ትልቁ ፣ ከሌንስ ጋር የታየው ነገር ትልቅ ይሆናል። ከ 0 እስከ 1 መካከል ያለው የ M እሴት ነገሩ ትንሽ እንደሚመስል ያመለክታል።

• የነገሮች አቅጣጫ።

  አሉታዊ እሴት የሚያመለክተው የተቀረፀው ምስል እንደሚገለበጥ ነው።

• እዚህ በተሰጠው ምሳሌ ፣ የ -0.666 ኤም እሴት ማለት አሁን ባለው ተለዋዋጭ እሴት መሠረት የአሻንጉሊት ጥላ ይታያል። ተገልብጦ እና ከትክክለኛው መጠን ሁለት ሦስተኛ ያነሰ.

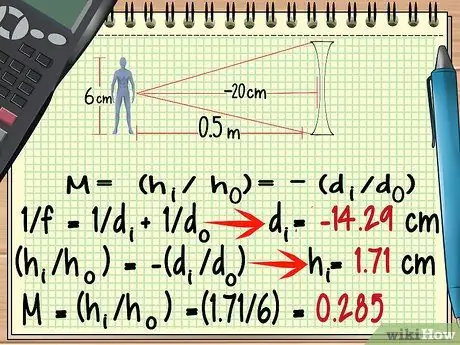
ደረጃ 6. ለተለዋዋጭ ሌንስ ፣ አሉታዊ የትኩረት ነጥብ ይጠቀሙ።

ምንም እንኳን የሚለያይ ሌንስ ቅርፅ ከተለዋዋጭ ሌንስ በጣም የተለየ ቢሆንም ፣ ከላይ ያለውን ተመሳሳይ ቀመር በመጠቀም ማጉላቱን ማስላት ይችላሉ። ልብ ሊሉት የሚገባቸው የማይካተቱ ሁኔታዎች አሉ የሚለየው ሌንስ የትኩረት ነጥብ አሉታዊ ነው።

ከላይ ባለው የምሳሌ ችግር ውስጥ ፣ ይህ በማስላት ላይ በሚያገኙት መልስ ላይ ተጽዕኖ ይኖረዋል_እኔ፣ ስለዚህ ለዚህ ትኩረት መስጠቱን ያረጋግጡ።

• ከላይ ያለውን የምሳሌ ችግር እንደገና እንሥራ ፣ አሁን እኛ የትኩረት ርዝመት ያለው የተለየ ሌንስ እንጠቀማለን - 20 ሴ.ሜ.

  ሌሎቹ ተለዋዋጮች ተመሳሳይ እሴት ሆነው ይቆያሉ።

• በመጀመሪያ ፣ እኛ እንሰላለን መ_እኔ የሌንስ እኩልታን በመጠቀም;

  1/f = 1/መ_o + 1/መ_እኔ

  1/-20 = 1/50 + 1/መ_እኔ

  -5/100 - 2/100 = 1/መ_እኔ

  -7/100 = 1/መ_እኔ

  -100/7 = መ_እኔ = - 14 ፣ 29 ሳ.ሜ

• አሁን ሸን እናሰላለን_እኔ እና ኤም ከ d እሴት ጋር_እኔ አዲሱ።

  (ሸ_እኔ/ሰ_o) = -(መ_እኔ/መ_o)

  (ሸ_እኔ/6) = -(-14, 29/50)

  ሸ_እኔ = -(-14, 29/50) x 6

  ሸ_እኔ = 1 ፣ 71 ሳ.ሜ

  መ = (ሸ_እኔ/ሰ_o)

  መ = (1, 71/6) = 0, 285

ዘዴ 2 ከ 2 - የብዙ ሌንሶችን ማጉላት ማስላት

ቀላል የሁለት ሌንስ ዘዴ

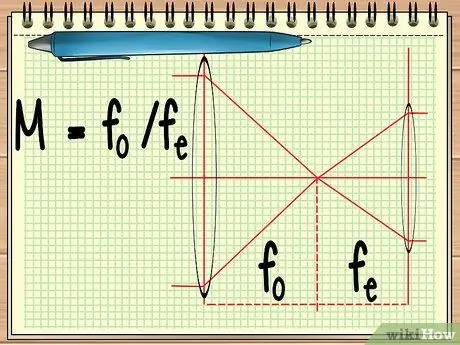
ደረጃ 1. የሁለቱን ሌንሶች የትኩረት ነጥብ ያሰሉ።

እርስ በእርስ የተስተካከሉ ሁለት ሌንሶችን (እንደ ቴሌስኮፕ ወይም ጥንድ ቢኖክዮላር) ያካተተ መሣሪያ ሲጠቀሙ ፣ ማወቅ ያለብዎት የሁለቱን ሌንሶች አጠቃላይ ማጉላት ለማስላት የሁለቱ ሌንሶች የትኩረት ነጥብ ነው። ይህ በቀላል ቀመር M = f ሊሰላ ይችላል_o/ረ_ሠ.

በቀመር ውስጥ ፣ ረ_o የዓላማ ሌንስ የትኩረት ነጥብ እና ረ_ሠ የዓይን መነፅር የትኩረት ነጥብ ነው። ተጨባጭ ሌንስ ከእቃው ጋር ቅርብ የሆነ ትልቅ ሌንስ ሲሆን የዓይን መነፅር ደግሞ ከተመልካቹ አይን አጠገብ የሚገኝ ሌንስ ነው።

ደረጃ 2. አስቀድመው ያለዎትን መረጃ ወደ ቀመር M = f ያስገቡ_o/ረ_ሠ.

የሁለቱም ሌንሶች የትኩረት ነጥቦችን ካገኙ በኋላ እነሱን ማስላት በጣም ቀላል ነው ፣ - የዓላማ ሌንስን የትኩረት ርዝመት በአይን መነፅር የትኩረት ርዝመት በመከፋፈል ጥምርታውን ያስሉ። እርስዎ የሚያገኙት መልስ የመሳሪያው አጠቃላይ ማጉላት ነው።

• ለምሳሌ ፣ አንድ ቀላል ቴሌስኮፕ እንበል ፣ የተፃፈው የዓላማ ሌንስ የትኩረት ነጥብ 10 ሴ.ሜ እና የዓይን መነፅሩ የትኩረት ነጥብ 5 ሴ.ሜ ነው ፣ ከዚያ ማጉላት 10/5 = 2.

  የተወሳሰበ ዘዴ

  

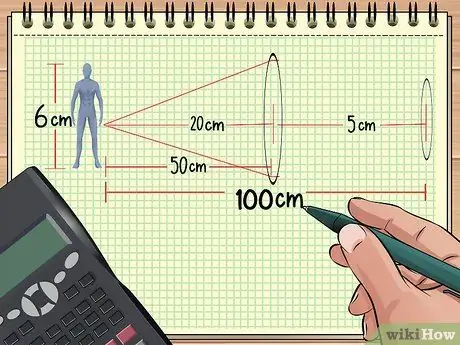
  ደረጃ 1. በሌንሶች እና በእቃው መካከል ያለውን ርቀት ያሰሉ።

  በአንድ ነገር ፊት በተከታታይ የተደረደሩ ሁለት ሌንሶች ካሉዎት ፣ ከሌንሶች እስከ ነገሩ ያለውን ርቀት ፣ የእቃውን መጠን እና የሁለቱን ሌንሶች የትኩረት ነጥብ ካወቁ አጠቃላይ ማጉላት ሊሰላ ይችላል። ቀሪው እንዲሁ ሊሰላ ይችላል።

  ለምሳሌ ፣ ከላይ በምሳሌው ችግር 1 ውስጥ ነገሮችን እና ሌንሶችን እናዘጋጃለን እንበል - አሻንጉሊት 20 ሴንቲ ሜትር የትኩረት ርዝመት ካለው ከተገጣጠመው ሌንስ 50 ሴ.ሜ ነው። አሁን ሁለተኛውን ሌንስ ከትኩረት ነጥብ 5 ሴ.ሜ ጋር ከመጀመሪያው ሌንስ በ 50 ሴ.ሜ ርቀት (ከአሻንጉሊት 100 ሴ.ሜ.) ከዚህ በኋላ ያገኘነውን መረጃ በመጠቀም አጠቃላይ ማጉላትን እናሰላለን።

  

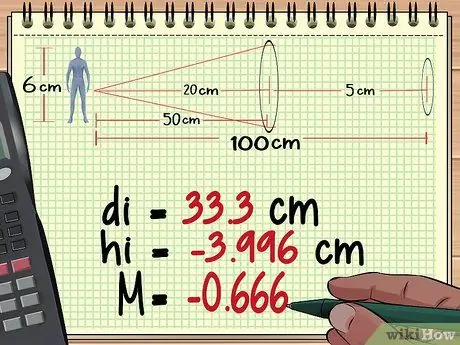
  ደረጃ 2. የነገሩን ርቀት ፣ ቁመት እና ማጉላት ከሌንስ 1 ያሰሉ።

  የብዙ ሌንሶችን ማጉላት የማስላት የመጀመሪያው ክፍል የአንድን ሌንስ ማጉላት ከመቁጠር ጋር ተመሳሳይ ነው። ወደ ነገሩ በጣም ቅርብ በሆነው ሌንስ ይጀምሩ ፣ ከተሠራው ምስል ርቀትን ለማግኘት የሌንስ ቀመር ይጠቀሙ ፣ ከዚያ የምስሉን ቁመት እና ማጉላት ለማግኘት የማጉላት ቀመር ይጠቀሙ። ተጨማሪ ነጠላ ሌንስ ማጉያ ስሌቶችን ለማየት እዚህ ጠቅ ያድርጉ።

  • ከላይ ባለው ዘዴ 1 ውስጥ ካሉት ስሌቶቻችን ፣ የመጀመሪያው ሌንስ ምስልን ከፍ የሚያደርግ ሆኖ እናገኘዋለን - 3 ፣ 996 ሳ.ሜ ፣ ርቀት 33.3 ሴ.ሜ ከሌንስ በስተጀርባ ፣ እና በማጉላት ላይ - 0, 666.

    

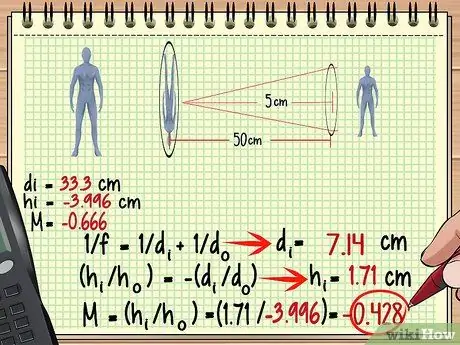
    ደረጃ 3. ምስሉን ከመጀመሪያው ሌንስ እንደ ሁለተኛው ዕቃ እንደ ዕቃ ይጠቀሙ።

    አሁን ፣ ለሁለተኛው ሌንስ ማጉላትን ፣ ቁመትን እና ሌሎችን ማግኘት በጣም ቀላል ነው - ልክ ለመጀመሪያው ሌንስ የተጠቀሙበትን ተመሳሳይ ዘዴ ይጠቀሙ ፣ ብቻ ፣ በዚህ ጊዜ ምስሉን እንደ ዕቃ ይያዙት። ወደ ሁለተኛው ሌንስ የምስል ርቀቱ ሁል ጊዜ ከመጀመሪያው ሌንስ ጋር ካለው የነጥብ ርቀት ጋር እንደማይመሳሰል ያስታውሱ።

    • ከላይ ባለው ምሳሌ ፣ ምስሉ ከመጀመሪያው ሌንስ በስተጀርባ 33.3 ሴ.ሜ ስለተፈጠረ ፣ ርቀቱ 50-33.3 = ነው 16.7 ሳ.ሜ በሁለተኛው ሌንስ ፊት። በሁለተኛው ሌንስ የተሰራውን ምስል ለማግኘት ይህንን ልኬት እና የሁለተኛውን ሌንስ የትኩረት ርዝመት እንጠቀም።

      1/f = 1/መ_o + 1/መ_እኔ

      1/5 = 1/16 ፣ 7 + 1/መ_እኔ

      0, 2 - 0, 0599 = 1/መ_እኔ

      0 ፣ 14 = 1/መ_እኔ

      መ_እኔ = 7 ፣ 14 ሳ.ሜ

    • አሁን ሸን ማስላት እንችላለን_እኔ እና ኤም ለሁለተኛው ሌንስ

      (ሸ_እኔ/ሰ_o) = -(መ_እኔ/መ_o)

      (ሸ_እኔ/-3, 996) = -(7, 14/16, 7)

      ሸ_እኔ = -(0, 427) x -3, 996

      ሸ_እኔ = 1 ፣ 71 ሳ.ሜ

      መ = (ሸ_እኔ/ሰ_o)

      M = (1 ፣ 71/-3 ፣ 996) = - 0, 428

    

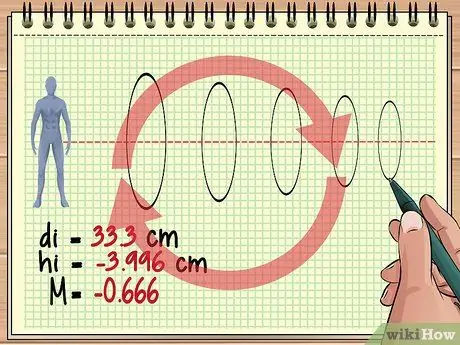
    ደረጃ 4. ለተጨማሪ ሌንሶች እንደዚህ ማስላትዎን ይቀጥሉ።

    በአንድ ነገር ፊት ሶስት ፣ አራት ወይም በመቶዎች የሚቆጠሩ ሌንሶች ካሉ ይህ መሠረታዊ አካሄድ ተመሳሳይ ነው። ለእያንዳንዱ ሌንስ ፣ የቀደመውን ሌንስ ምስል እንደ ዕቃው አድርገው ይቆጥሩት እና የሚፈልጉትን መልስ ለማግኘት የሌንስ እኩልታን እና የማጉላት እኩልታን ይጠቀሙ።

    እያንዳንዱ ቀጣይ ሌንስ የተቀረፀውን ምስል ያለማቋረጥ ሊቀይር እንደሚችል ያስታውሱ። ለምሳሌ ፣ ቀደም ሲል ያገኘነው የማጉላት እሴት (-0 ፣ 428) እኛ የምናየው ምስል በግምት 4/10 የእቃው መጠን በግምት 4/10 መሆኑን ያሳያል ፣ ግን ቀጥ ያለ ነው ፣ ምክንያቱም ከቀዳሚው ሌንስ የመጣ ምስል ተገልብጧል።

    ጠቃሚ ምክሮች

    • ቢኖክለሮች ብዙውን ጊዜ የማጉላት ዝርዝሮችን በሌላ ቁጥር በቁጥር መልክ ማብራሪያ ይሰጣሉ። ለምሳሌ ፣ ቢኖኩላሮች 8x25 ወይም 8x40 ተብለው ሊገለጹ ይችላሉ። እንደዚያ ሲፃፍ የመጀመሪያው ቁጥር የቢኖኩላሮች ማጉላት ነው። በተሰጠው ምሳሌ ውስጥ ሁለቱ ቁጥሮች በመጠን ቢለያዩም ምንም አይደለም ፣ ሁለቱም ቢኖክዮላሮች 8 ጊዜ ማጉላት አላቸው። ሁለተኛው ቁጥር ምስሉ በቢኖኩላሮች ምን ያህል ግልፅ እንደሚሆን ያመለክታል።
    • ያስታውሱ ለነጠላ ሌንስ ሉፕ ፣ የነገሩ ርቀት ከሌንስ የትኩረት ርዝመት በላይ ከሆነ ማጉያው አሉታዊ ይሆናል። ይህ ማለት የተፈጠረው ምስል ያነሰ ይሆናል ማለት አይደለም። በዚህ ሁኔታ ፣ መስፋፋት አሁንም ይከሰታል ፣ ግን የተቀረፀው ምስል በተመልካቹ ተገልብጦ (ከላይ ወደ ታች) ይታያል።