የቁጥር ውሂብ ሁነታን እንዴት ማግኘት እንደሚቻል - 8 ደረጃዎች (ከስዕሎች ጋር)

2024 ደራሲ ደራሲ: Jason Gerald | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2024-01-15 08:08

በስታቲስቲክስ ውስጥ ፣ ሁነታው በቁጥሮች ወይም በውሂብ ስብስብ ውስጥ ብዙውን ጊዜ የሚታየው ቁጥር ነው። ውሂቡ ሁል ጊዜ አንድ ሁናቴ ብቻ የለውም ፣ ሁለት ወይም ከዚያ በላይ ሊሆን ይችላል (ስለዚህ ባለ ሁለትዮሽ ወይም ባለብዙ ሞዳል ተብሎ ይጠራል)። በሌላ አነጋገር ፣ በውሂብ ውስጥ ብዙ ጊዜ የሚከሰቱ ሁሉም ቁጥሮች እንደ ሞድ ሊጠሩ ይችላሉ። ሁነታን እንዴት ማግኘት እንደሚችሉ ለማወቅ ከዚህ በታች ያሉትን ደረጃዎች ይከተሉ።

ደረጃ

ዘዴ 1 ከ 2 - የውሂብ ሁነታን መፈለግ

ደረጃ 1. በውሂብ ውስጥ ያሉትን ቁጥሮች ይፃፉ።

ሁነታው ብዙውን ጊዜ ከስታቲስቲክስ መረጃ ወይም ከቁጥሮች ዝርዝር ይወሰዳል። ስለዚህ ሁነታን ለማግኘት ውሂብ ያስፈልግዎታል። ውሂቡ በጣም ትንሽ ካልሆነ በስተቀር በአይምሮዎ ውስጥ ብቻ በማየት እና በመተንተን ሞዱን ማግኘት በጣም ከባድ ስለሆነ በመጀመሪያ መረጃውን እንዲመዘግቡ ወይም እንዲጽፉ ይመከራል። ወረቀት እና እርሳስ ወይም ብዕር የሚጠቀሙ ከሆነ ፣ በኋላ ላይ ለማስተካከል መጀመሪያ ውሂቡን ይፃፉ። ኮምፒውተር ላይ ከሆኑ ፣ በኋላ ላይ በራስ -ሰር ለመደርደር የተመን ሉህ ፕሮግራም መጠቀም ይችላሉ።

ከምሳሌ ችግር ከተከተልን የውሂብ ሁነታን የማግኘት ሂደት ለመረዳት ቀላል ነው። ለአሁን ፣ ይህንን የናሙና ውሂብ እንጠቀም - {18, 21, 11, 21, 15, 19, 17, 21, 17}. በሚቀጥሉት ጥቂት ደረጃዎች ውስጥ ሁነታን እናገኛለን።

ደረጃ 2. ቁጥሮቹን ከትንሽ እስከ ትልቁ ደርድር።

ውሂብን መደርደር በእውነቱ ሊከናወን አይችልም። ነገር ግን ይህ እርምጃ በእውነቱ ሁነቱን እንዲያገኙ ይረዳዎታል ምክንያቱም ተመሳሳይ ቁጥሮች እርስ በእርስ ስለሚቆጠሩ ለማስላት ቀላል ያደርጉታል። የውሂብዎ መጠን በጣም ትልቅ ከሆነ ፣ ለስህተት ተጋላጭ የሆነውን የመከሰት መጠን ለመቀነስ ይህ እርምጃ መወሰድ አለበት።

• ወረቀት እና እርሳስ ወይም ብዕር የሚጠቀሙ ከሆነ ቀደም ብለው የጻፉትን ውሂብ በቅደም ተከተል ይፃፉ። ከመረጃው ትንሹን ቁጥር በማግኘት ይጀምሩ። ካገኙት በአዲስ መስመር ላይ ይፃፉት ፣ ከዚያ በቀደመው የውሂብ ዝርዝር ውስጥ ያለውን ቁጥር ያቋርጡ። የሚቀጥለውን አነስተኛ ቁጥር ይፈልጉ እና ሁሉንም ቁጥሮች እስኪያስተካክሉ ድረስ ተመሳሳይ ነገር ያድርጉ።
• የተመን ሉህ ፕሮግራም በኮምፒተርዎ ላይ ከተጠቀሙ የቁጥሮችን ዝርዝር በጥቂት ጠቅታዎች ብቻ መደርደር ይችላሉ።

• ከላይ ባለው ምሳሌአችን ውስጥ የተደረደረው መረጃ ነው {11, 15, 17, 17, 18, 19, 21, 21, 21}.

  

  ደረጃ 3. አንድ ቁጥር የሚታየውን ብዛት ይቁጠሩ።

  ለአነስተኛ መረጃ ፣ በቀላሉ የተደረደረውን ውሂብ ማየት ይችላሉ ፣ ከዚያ የትኛው ቁጥር እዚያ እንደሚታይ ይፈልጉ። የእርስዎ ውሂብ ትልቅ ከሆነ ፣ ከዚያ ስህተቶችን ለማስወገድ አንድ በአንድ ማስላት አለብዎት።

  • የተሳሳቱ ስሌቶችን ለማስወገድ ወረቀት እና እርሳስ ወይም ብዕር የሚጠቀሙ ከሆነ እያንዳንዱ ቁጥር ስንት ጊዜ እንደሚታይ ያስተውሉ። የተመን ሉህ በኮምፒተር ላይ የሚጠቀሙ ከሆነ ፣ በሌላ ዓምድ ውስጥ መቅዳትም ይችላሉ ፣ ወይም የሚያውቁ ከሆነ በፕሮግራሙ ውስጥ የቀረቡትን ቀመሮች መጠቀም ይችላሉ።
  • በምሳሌው ችግር ማለትም ({11 ፣ 15 ፣ 17 ፣ 17 ፣ 18 ፣ 19 ፣ 21 ፣ 21 ፣ 21}) ፣ ቁጥር 11 አንድ ጊዜ ይታያል ፣ 15 አንድ ጊዜ ይከሰታል ፣ 17 ሁለት ጊዜ ይከሰታል ፣ 18 አንዴ ይከሰታል ፣ 19 አንዴ ይከሰታል ፣ እና 21 ሦስት ጊዜ ይታያል. ከዚያ በመነሳት ፣ ብዙ ጊዜ የሚታየው ቁጥር 21 መሆኑ ግልፅ ነው።

  

  ደረጃ 4. ብዙውን ጊዜ የሚታየው ቁጥር የውሂብ ሞድ ነው።

  እያንዳንዱ ተመሳሳይ ቁጥሮች ስንት ጊዜ እንደሚታዩ ካስተዋሉ በኋላ አስቀድመው ማወቅ አለብዎት የትኛው ቁጥር በብዛት ይታያል ፣ ማለትም የውሂብ ሁናቴ ማለት ነው. ያንን ያስታውሱ አንድ ውሂብ ከአንድ በላይ ሞድ ሊኖረው ይችላል. አንድ ውሂብ ሁለት ሁነታዎች ካሉ ፣ ውሂቡ ቢሞዳዳል ተብሎ ሊጠራ ይችላል ፣ ሶስት ሁነታዎች ካሉ ፣ ትሪሞዳዳል ፣ ወዘተ.

  • በምሳሌው ችግር ውስጥ ፣ ሁነታው 21 ነው ምክንያቱም በጣም በተደጋጋሚ ይታያል።
  • እሱ ሌላ ሶስት ጊዜ የሚታየው ሌላ ቁጥር ካለ ፣ ከዚያ 21 እና ያ ቁጥር ሞድ ነው።

  

  ደረጃ 5. የውሂብ ሁነታን በመካከለኛ (አማካይ) እና በመሃከለኛነት ይለዩ።

  ሦስቱ የስታቲስቲክስ ጽንሰ -ሀሳቦች ብዙውን ጊዜ በአንድ ውይይት ውስጥ ይወያያሉ። ተመሳሳይ ስሞች ስላሏቸው እና አንዳንድ ጊዜ ተመሳሳይ እሴት ስለሚኖራቸው ፣ ብዙ ሰዎች እነሱን መለየት አስቸጋሪ ሆኖባቸዋል። ሆኖም ፣ ምንም እንኳን አንድ ውሂብ አንድ ዓይነት ሞድ ፣ መካከለኛ ወይም አማካይ ቢኖረውም ፣ እነሱ የተለዩ መሆናቸውን እና ለብቻቸው መቆማቸውን ያስታውሱ። ማብራሪያውን ከዚህ በታች ያንብቡ።

  • አማካይ ማለት አማካይ ማለት በመረጃ ቁጥር የተከፈለ የውሂብ እሴቶች ድምር ነው። ለምሳሌ ፣ በምሳሌው ችግር ({11 ፣ 15 ፣ 17 ፣ 17 ፣ 18 ፣ 19 ፣ 21 ፣ 21 ፣ 21}) ፣ አጠቃላይ መረጃው 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 = 160. እና በመረጃው ውስጥ 9 እሴቶች ስላሉ ፣ ከዚያ 160/9 = 17.78.

    

  • ውሂቡ ከተደረደረ እና ጥቃቅን እና ትልልቅ እሴቶችን ከመረጃው ከተለየ በኋላ ሚዲያው መካከለኛ እሴት ነው። በምሳሌው ችግር ፣ ({11 ፣ 15 ፣ 17 ፣ 17 ፣ 18 ፣ 19 ፣ 21 ፣ 21 ፣ 21}) ፣ ሚዲያው

    ደረጃ 18። ምክንያቱም ቁጥሩ መሃል ላይ ነው ፣ እና በመረጃው ውስጥ አራት ቁጥሮች ከፍ እና አራት ቁጥሮች ከ 18 በታች ናቸው። ውሂቡ እኩል ቁጥር ከሆነ ፣ ሚዲያው በመሃሉ ላይ ያሉትን የሁለት ቁጥሮች ድምር በማስላት ከዚያም በሁለት በመከፋፈል ያገኛል።

    

  ዘዴ 2 ከ 2 - ሞድ በልዩ ችግር ውስጥ መፈለግ

  

  ደረጃ 1. በመረጃው ውስጥ ያሉት ሁሉም ቁጥሮች አንድ ዓይነት የክስተቶች ብዛት ካላቸው አንድ ውሂብ ምንም ሁነታ የለውም።

  ለምሳሌ ፣ ሁሉም ቁጥሮች አንድ ጊዜ ብቻ ቢታዩ ፣ ውሂቡ ሁነታ የለም ምክንያቱም ሁለቱም ቁጥሮች ከሌላው በበለጠ በተደጋጋሚ አይታዩም። ሁሉም ቁጥሮች ሁለት ጊዜ ወይም ከዚያ በላይ ቢታዩ ተመሳሳይ ነው።

  ከላይ ባለው ምሳሌ ችግር ውስጥ ያለውን ውሂብ ወደ {11 ፣ 15 ፣ 17 ፣ 18 ፣ 19 ፣ 21} ከቀየርነው ፣ ይህ ማለት ሁሉም ቁጥሮች አንድ ጊዜ ብቅ ይላሉ ፣ ከዚያ ውሂቡ ምንም ሁነታ የለውም ፣ እንዲሁም ውሂቡ ወደ {11 ከተለወጠ ፣ 11 ፣ 15 ፣ 15 ፣ 17 ፣ 17 ፣ 18 ፣ 18 ፣ 19 ፣ 19 ፣ 21 ፣ 21}።

  

  ደረጃ 2. ቁጥራዊ ያልሆነ ውሂብ አሁንም እንደ ቁጥራዊ ውሂብ ላሉት ሁነታው መፈለግ ይችላል።

  ብዙውን ጊዜ ውሂቡ በቁጥር ወይም በቁጥር መልክ ይገኛል ፣ ስለሆነም በብዙ ዘዴዎች ሊሠራ ይችላል። ሆኖም ፣ አንዳንድ ጊዜ በቁጥሮች መልክ ያልሆኑ ነገሮች አሉ። ሆኖም ፣ ይህ የውሂብ ሁኔታ በጣም በተደጋጋሚ የሚከሰተውን (በመረጃ መግለጫዎች መልክ ሊሆን ይችላል) በመፈለግ በቀላሉ ሊፈለግ ይችላል። ግን ቁጥራዊ ላልሆኑ መረጃዎች አማካይ ወይም መካከለኛ ማግኘት አይችሉም።

  • ለምሳሌ ፣ ባዮሎጂያዊ የዳሰሳ ጥናት እያደረጉ ነው እንበል ፣ ይህም በአካባቢዎ የትኞቹ የዛፍ ዝርያዎች እንደሚያድጉ ለማወቅ ነው። ያገኙት ውሂብ {እሳት ፣ ማንጎ ፣ ስፕሩስ ፣ ፓልም ፣ ስፕሩስ ፣ ፊር ፣ ማንጎ ፣ ማንጎ ፣ ፓልም ፣ ፊር} ነው። እያንዳንዱ የውሂብ እሴት በስም ስለሚለይ እንደዚህ ያለ ውሂብ በስመ ውሂብ ይባላል። ለዚህ ምሳሌ ፣ ሁነታው ነው fir ምክንያቱም ብዙ ጊዜ (አምስት ጊዜ) ይታያል።
  • ምሳሌውን ከተመለከቱ ፣ አማካይ ወይም ሚዲያን ማስላት የሚችሉበት ምንም መንገድ የለም።

  

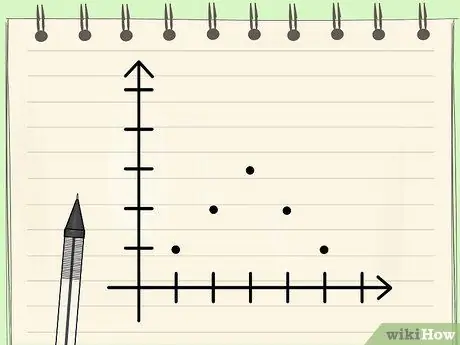
  ደረጃ 3. ለሲሞሜትራዊ (unimodal unimodal) የውሂብ ስርጭት ፣ የውሂብ ሞድ ፣ መካከለኛ እና አማካይ ተመሳሳይ እንደሚሆን ይወቁ።

  ቀደም ሲል እንደተጠቀሰው ፣ የውሂብ ስብስብ አማካይ ፣ መካከለኛ እና ሞድ አንድ ዓይነት የሚሆኑበት ጊዜያት ይኖራሉ። ከሁኔታዎች አንዱ መረጃው በጥብቅ የተመጣጠነ የእሴቶች ስርጭት ካለው (በስዕላዊ መልክ ከተሳሉ የጋውስ ደወል ቅርፅ ያለው ኩርባ ይፈጥራል)። ስርጭቱ የተመጣጠነ ስለሆነ ፣ እንደዚህ ያለ የውሂብ ሁኔታ ብዙውን ጊዜ የሚታየው ውሂብ መሆን አለበት ፣ እና መካከለኛው እሴት ስለሆነ ፣ ቁጥሩ እንዲሁ መካከለኛ ነው ማለት ነው. እና ሂሳብን ከሠሩ ፣ አማካዩ ተመሳሳይ ቁጥር ያስገኛል።

  • ለምሳሌ ፣ ከውሂብ {1 ፣ 2 ፣ 2 ፣ 3 ፣ 3 ፣ 3 ፣ 4 ፣ 4 ፣ 5} ፣ ግራፉን ከሳሉ ፣ የፓራቦላ ግራፍ ያገኛሉ። የውሂብ ሞድ 3 ነው ብዙውን ጊዜ ስለሚታይ ፣ መካከለኛ 3 ነው ምክንያቱም ቁጥሩ መሃል ላይ ነው ፣ እና አማካይ 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3 ነው.
  • እንደዚህ ያሉ ጉዳዮች ልዩ ሁኔታዎች አሏቸው ፣ ማለትም ይህ የተመጣጠነ መረጃ ከአንድ በላይ ሁናቴ ሲኖረው። ይህ ከሆነ ፣ አማካዩ እና ሚዲያን ከአንድ እሴት በላይ ሊሆኑ ስለማይችሉ ፣ ሁነታው ከመካከለኛው እና ከመካከለኛው ጋር አንድ አይሆንም።

  ጠቃሚ ምክሮች

  • አንድ ውሂብ ከአንድ በላይ ሁነታዎች ሊኖረው ይችላል
  • በአንድ ውሂብ ውስጥ የሁሉም ቁጥሮች ክስተቶች ብዛት አንድ ከሆነ የውሂብ ሁናቴ የለም።